이번에는 각운동량에 대한 이야기를 할 차례인데, 선형 운동량이 여러모로 중요한 입자를 가졌던것과 같이 각운동량도 그와 동등한 수준의 입지를 갖는 개념이다.
선형 운동량이 보존됐던 것 처럼 각운동량도 고립계의 경우 보존되며, 두 보존법칙은 상대론과 양자역학에도 적용 가능할만큼 폭넓게 응용된다.
피겨 선수들이 제자리에서 회전 할 때, 팔이나 다리를 오므려서 회전 반경을 줄일수록 더 빠르게 돌게되는 이유를 알 수 있는 부분이기도 하다.
11.1 벡터 곱 (외적) 과 토크 The Vector Product and Torque
회전운동에 대한 이야기에서 우리는 아래의 그림을 봤었고,
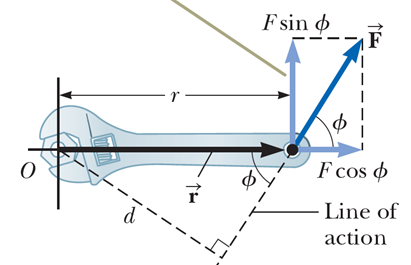
여기서 토크의 크기를 다음과 같이 정의했다.

그런데, r 과 F 가 모두 벡터이고, 두 벡터의 크기와 그 사잇각의 사인의 곱은 벡터 연산에서 벡터곱 (외적) 이라 부르는 계산과 같은 과정이기 때문에 우리는 토크를 아래와 같은 형태로 다시 정의 할 수 있다.

벡터곱의 결과 역시 벡터이기 때문에 방향을 갖게 되는데 그 방향은
오른손 손바닥을 펴고, 엄지를 제외한 네 손가락을 r 의 방향에서 F 의 방향으로 말아 쥐었을 때 엄지가 향하는 방향 으로 정한다. 아래 그림과 같이.

계산해야 하는 두 벡터가 3차원 성분으로 주어지면 다음과 같이 행렬식을 이용한 계산을 해서 그 값을 얻을 수 있다.
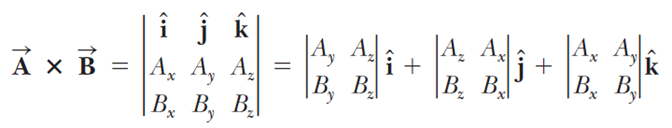

여기서는 벡터곱으로 토크를 정의하는것과 아주 기본적인 계산 방법만 알아보기로 하자.
벡터 자체에 대한 내용, 단위벡터들의 관계와 같은 수학적인 내용은 교재의 11.1 을 참고하거나 다른 수학책을 통해 각자 알아보기로 하고.
[참고문헌]
주 교재 : Physics for Scientists and Engineers, 9th Edition, Serway/Jewett