그림으로 시작.

얼음판 위에 아주 단단히 고정되어 있는 기둥을 향해서 달려오던 스케이트 선수가 기둥을 지나치는 순간 팔을 뻗어서 기둥을 붙들면 스케이트 선수는 기둥 근처를 회전하는 운동을 하게 된다.
선형 운동량의 개념이 병진운동을 이해하고 분석하는데 유용했듯 이제 알아볼 각운동량은 위 스케이터와 같은 물체의 회전 운동을 이해하는데 도움이 된다.
선형 운동량을 다룰 때와 유사한 과정으로 각운동량에 대한 이야기를 시작해보자.

위 그림과 같이 질량 m 인 물체가 원점으로부터 r 의 위치 (vector position) 에서 p 의 선형 운동량을 갖고 움직인다고 하자.
병진운동을 다루는 중 이라면 이 물체에 가해지는 힘은 선형운동량 p 의 순간변화율을 통해 다음의 식 으로 구할 수 있다.

그런데, 물체에 가해지는 힘과 위치의 벡터곱이 토크임은 이미 알고있으니까, 우리는 위 식에 아래와 같은 과정을 적용 해볼 수 있다.

이제 수학적인 트릭을 약간 써먹을건데, 1+0=1 과 같이 위 식의 우변에 0 을 더하는 작업을 할거다.
0을 더한다니, 이게 무슨 되도않는 소린가 싶겠지만, 0을 더하거나 1을 곱하는 것 같은 트릭을 물리에서는 종종 이용한다.
그래서, 0 을 더하는 효과를 위해 우리는 위 식의 우변에 다음을 더할거다.

우변의 식과 r, p 는 동일한데 미분기호가 r 에 붙었다는게 달라졌고, dr/dt 는 속도(v)가 되는데, 속도(v)는 선형운동량 p 와 방향이 같아서, 결국 위의 값은 r 과 p 에 관계없이 항상 0 이다.
물론 곱하기는 벡터곱 이다.
이제 이 사실을 위의 원래 토크에 대한 식에 대입하면,

짠.
더하기의 앞은 원래 있던 항이고, 뒤에 뭔가를 보탰지만 그 값은 항상 0 이라 식의 형태만 바뀌었을 뿐 동일한 결과를 얻을 수 밖에 없는 새로운 식이 만들어졌다. 1+0=1 을 한 것.
이 형태에서 우리는 우변을 다음의 벡터 연산법칙을 통해 하나의 식으로 간단히 쓸 수 있다.


위 식은 다음의 힘과 선형운동량의 관계와 “대충” 유사한 형태인데,

병진운동에서 물체에 작용하는 힘의 크기는 선형 운동량의 미분으로 알 수 있고, 회전운동에서 토크는 선형 운동량과 무언가 관계가 있는 값의 미분으로 구 할 수 있다.
다르게 표현하면, 병진운동에서 힘이 하던 역할을 회전운동에서는 토크가 수행하는데, 이와 유사하게 병진운동에서 운동량 p 가 하던 역할을 회전운동에서는 r x p 가 수행한다. 라고 이해해도 괜찮다는 말 이고,
이를 바탕으로 우리는 회전하는 물체의 각운동량 L 을 다음으로 정의 한다.

원점 O 를 관통하는 축에 대해 회전하는 입자의 각운동량 L 은 입자의 순간 위치 벡터 r 과 순간 선형 운동량 p 의 벡터곱으로 정의한다.
이제 우리는 회전운동하는 물체에 가해지는 토크를 각운동량으로 다음으로 쓸 수 있고, 이는 뉴턴의 두번째 운동법칙을 통한 회전운동의 기술이다.

힘의 작용이 선형 운동량을 변화 시켰듯 토크의 작용은 각운동량을 변화시킨다.
“고정된 축에 대한 강체의 회전” 이라는 표현 처럼, 우리는 회전운동을 다룰 때 어떤 축에 대한 운동인가를 주의깊게 확인해야 한다.
마찬가지로 각운동량을 통한 토크의 정의 역시 토크와 각운동량이 동일한 축에 대한 이야기 일 때 성립한다.
SI 단위계에서 각운동량은 kg m^2/s 의 단위를 갖는다. 선형 운동량의 단위에 미터(m) 가 한번 더 곱해진 형태인데, 이는 r 과의 벡터곱에서 발생하는 효과다.
아래 그림을 다시 보면,

각운동량은 벡터 r 과 p 를 포함하는 평면에 항상 수직이고, 따라서 r 과 p 가 평행하면 각운동량은 0 이 된다.
여러 입자로 이루어진 계의 각운동량 – Angular momentum of a system of particles
선형 운동량에 대한 이야기를 하면서 우리는 지금과 마찬가지로 비고립계의 경우를 알아봤었는데, 거기서 다음의 결과를 얻었었다.

여러 입자로 이루어진 계에 작용한 외력의 합은 계를 이루는 입자의 전체 선형 운동량의 미분으로 구할 수 있다.
이 내용이 여러 입자로 이루어진 계의 각운동량과는 어떤 관계가 있는지 알아보자.
먼저, 임의의 축에 대한 다입자 계의 전체 각운동량은 계를 이루는 입자 각각의 각운동량의 합과 같다.

이 값의 시간에 대한 미분은 다음의 형태가 된다.

계의 내부에서 입자 사이에 작용하는 토크는 작용-반작용에 의해 0 이 된다는 즉, 계 내부의 모든 힘에 의한 토크는 0 이라는 사실을 “적당히” 받아들이면 우리는 다음 결론을 얻게된다.
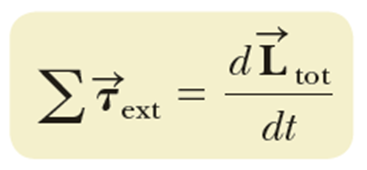
계의 전체 각운동량의 변화는 순전히 계의 외부에서 작용하는 순 토크 (net torque) 에 의해서 발생한다.
그리고 이를 비고립계의 각운동량 해석 정도로 표현 할 수 있다.
이번 내용은 여기까지이고, 다음에는 회전하는 물체의 각운동량에 대한 이야기를 해보자.
[참고문헌]
주 교재 : Physics for Scientists and Engineers, 9th Edition, Serway/Jewett