이제 평면을 따라 굴러가는 운동에 대한 이야기를 해볼건데, 방바닥에 동전을 굴린 것 같은 형태의 운동이고, 이 운동은 아래 그림처럼 다소 복잡한 운동이다.
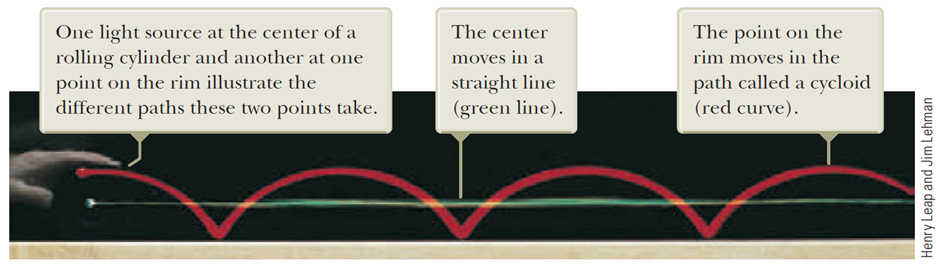
우리는 위 그림의 녹색과 빨간색선이 무엇을 의미하는지 대충 알고 있는데, 녹색은 회전 운동의 축의 이동 경로를 표현한 선 이고, 빨간색은 물체(동전)의 테두리의 특정 위치가 어떤 경로를 따라 움직이는지 나타낸 선 이다.
빨간선과 같은 경로를 사이클로이드(cycloid) 라고 부르는데, 우린 굴러가는 운동을 이제 알아보기 시작했으니까 질량 중심의 운동, 즉 녹색선에 대한 이야기를 먼저 하기로 하자.
여기서 잠시, 우리는 언젠가부터 운동하는 물체가 강체 (rigid body) 임을 가정해왔는데, 왜 굳이 강체여야 하는지에 대해서 짧게 얘기하자면,
모든 물체는 힘이 가해지면 변형이 일어난다. 물체에 변형이 일어났다는건 가해진 힘의 일부가 물체의 형태를 바꾸는데 사용됐다는것이고, 그만큼의 힘은 물체의 운동에는 영향을 주지 못한다는 말이 된다.
우리는 지금 물체의 운동 에 대한 이야기를 하고 있는데, 만약 우리가 물체에 가해준 힘이 모두 물체의 운동에 영향을 주지 않는다면, - 아주 작은 힘이라도 물체의 변형으로 소비된다면 – 지금 이야기들로 얻는 수식을 비롯한 관계들은 변형에 소비된 힘의 크기 만큼의 오차를 갖게 된다.
이런 오차를 무시하고, (물론 가능한 수준에서) 힘과 운동의 관계를 다루고자 변형이 일어나지 않는 물체인 강체 라는 개념을 도입해서 사용하고 있는 것이다.
이러한 과정 역시 근사 (approximation) 를 바탕으로 하는 것이며, 근사에 대한 이야기는 예전에 올린 글을 참고하는것도 좋다.
이제 굴러가는 운동에 대한 이야기로 돌아와서,
굴러가는 물체가 미끄러지지 않고 온전히 굴러가기만 한다는 가정을 하면, 물체의 회전과 병진 운동 사이에 어떤 관계가 있는지 알 수 있다.
아래 그림처럼 R 의 반지름을 갖는 물체가 평면위를 굴러가고 있다면,

물체가 세타의 각만큼 회전하는 동안 물체의 질량 중심은 s 만큼의 병진운동을 하게 될텐데, 질량 중심의 이동거리 s 는 다음으로 쓸 수 있다.

각도는 물론 라디안이다.
그러면 질량 중심의 병진운동 속도는 다음으로 쓸 수 있다.
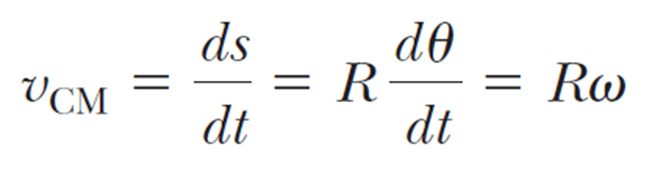
반지름 R 은 상수라서 미분기호 밖으로 빠져 나왔고, 오메가는 굴러가는 물체의 각속도인데, 왠지 한줄의 식으로 병진운동과 회전운동이 등호로 연결됨을 알 수 있다.
위 관계에서 질량 중심의 가속도가 어떻게 표현되는지까지 알아보면,

역시 반지름 R은 상수라서 미분기호 밖으로 나왔고, 알파는 굴러가는 물체의 각가속도 이다.
이번엔 아래 그림과 함께 굴러가는 물체의 운동을 회전운동과 병진운동으로 나눠서 생각해보자.
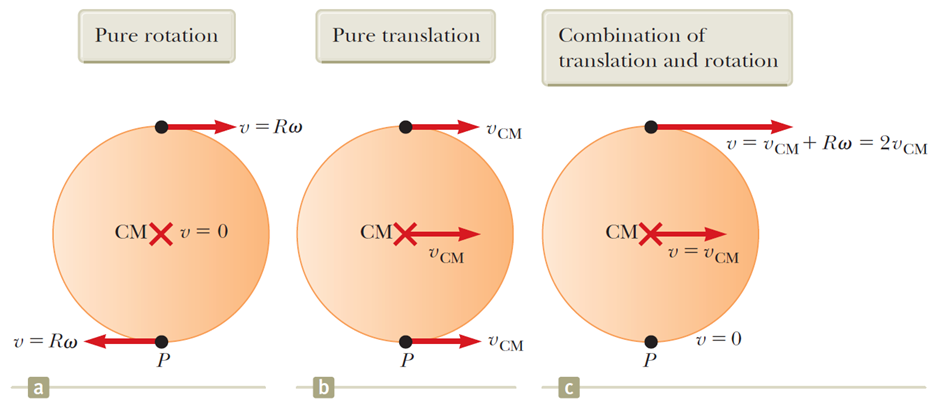
우리가 질량중심과 같은 속도로 움직이면서 물체를 보면, 물체는 위치의 이동 없이 축을 중심으로 회전하기만 하는것으로 보일텐데, 이는 위 그림의 a 와 같은 상황이다. 다시 말하면, 물체가 병진운동은 하지 않고 회전운동만 하는 상황이라고 생각해도 괜찮다는 이야기.
그림 b 는 물체가 회전하지 않고 병진운동만 하는 상황인데, 이때 물체의 모든 지점은 질량중심과 같은 속도로 움직일거다.
우리가 물체에 대해 상대적으로 정지해있는 상태에서 물체를 관찰한다면,
- 이렇게 쓰면 되게 어려운 말 같지만, 그냥 동전을 굴려놓고 얘가 어떻게 굴러가나 보고있다고 생각하면 된다. –
우리가 보는 동전의 운동은 위 그림의 회전운동 (a) 과 병진운동 (b) 이 동시에 발생하는 운동임을 알 수 있다. 즉, 동전의 어떤 특정 위치가 갖는 속도는 위 그림의 a 와 b 가 더해진 값을 갖게 된다는 이야기이고, 그림의 c 와 같은 결과를 얻게 될 거라는 말이다.
근데 그림 c 는 좀 이상한 부분이 있다, 분명 물체를 굴린다고 했고, 회전운동과 병진운동이 동시에 일어난다고 했는데, 바닥과 접촉하는 지점 P 의 속도가 0 이다. 이게 무슨 말이냐 대체.. 움직인다고 해놓고 속도가 없대.
물체 테두리의 특정 위치가 바닥과 만나는 지점을 지나는 순간 물체는 마치 접촉하고 있는 바닥이 없는 것 처럼 점 P 를 축으로 삼아 회전하듯 움직인다.
이게 또 무슨말이냐.. 바닥에서 굴러간다면서 바닥이 없는듯 움직인다니…
앞에서 본 그림에 동그라미와 화살표를 몇 개 추가해보면,

물체 테두리 특정위치의 움직임을 표시한 빨간 선을 쭉 따라가보면, 왠지 그 위치의 모든 회전은 왼쪽에서 오른쪽으로만 발생하고 있음을 알 수 있다.
“회전운동” 이면 분명 반대 방향으로 돌아가는 과정도 있어야 할텐데 그게 마치 안나타나는 것 같다는거지.
근데 이 효과가 회전 지점이 바닥면을 만나는 그 순간 발생한다는 이야기다. 그리고 이 현상이 마치 바닥면과 만나는 점 P 를 중심으로 물체가 회전한것과 같은 효과라는 말이다.
이는 물체 테두리의 특정 지점의 속도벡터를 가지고도 확인 할 수 있는데, 그림을 좀 그려보면,

노란색 화살표를 보면 역시 바닥을 만나는 지점을 통과하면서 반대방향의 회전이 사라진것 같은 현상이 일어남을 알 수 있다.
그럼 도대체 저 지점에서 실제로 무슨일이 일어나는지 알아보자.
그러기 위해서는 굴러가는 물체의 운동에너지를 먼저 생각해봐야 하는데,

관성모멘트 I 에 P 가 붙은건 점 P 를 관통하는 회전축에 대한 관성모멘트 이기 때문이다.
그리고 어찌됐든, P 를 축으로 상상의 회전을 하는 물체는 우리가 굴린 물체와 동일한 물체이니까, 실제로 굴러가는 물체와 동일한 운동에너지를 가질텐데, 그럼 위의 관성모멘트는 다음으로 바꿔 쓸 수 있다.

** 위 관계는 교재의 10.6 관성모멘트 계산 섹션 끝부분에 Parallel-axis theorem (평행축정리) 라는 이름으로 나와 있으니 계산과정등이 궁금한 사람은 참고하면 됨.
그러면 운동에너지는
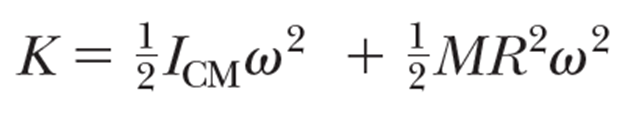
그런데 앞에서 우린 다음의 관계를 얻었으니까,
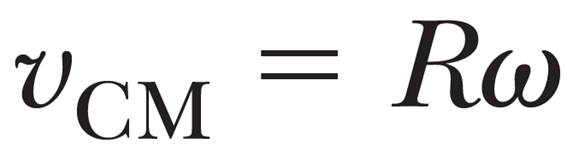
물체의 운동 에너지는 최종적으로 다음의 형태가 된다.
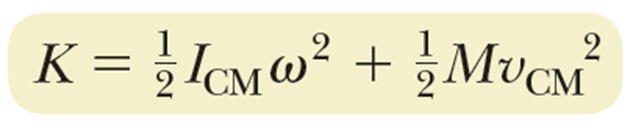
앞에서 우리는 굴러가는 운동을 회전운동과 병진운동의 조합 으로 접근해서 이야기를 진행 해 왔는데, 위 운동에너지의 식을 보면 그 접근이 옳다는 것을 확인 할 수 있다.
위 식 우변의 앞 항은 질량중심을 지나는 회전축을 중심으로 회전하는 물체의 회전운동 에너지 이고, 뒷 항은 질량중심의 병진운동의 운동에너지를 나타냄을 확인 할 수 있다.
그래서 저 식이 점 P 에서 일어나는 일과 무슨 관련이냐 할 수 있을텐데,
위 식을 다시 보면, 우변의 오른쪽 항은 질량중심의 속도를 포함하는데 (v cm), 점 P 에서 질량중심의 속도는 0 이었다.
그럼 모든 운동에너지가 물체의 회전을 발생시키는 효과만 남는데, 저 식은 점 P 를 회전축으로 갖는 물체의 관성모멘트로부터 얻어진 식이다.
그럼 뭐다? 물체의 모든 운동에너지가 점 P 를 중심으로 하는 회전운동에 기여했다. 는 말이 된다는 것.
여기까지면 물체가 굴러가는 운동을 어떻게 접근하고 이해해야 할지에 대한 이야기는 끝이다. 교재에는 rolling friction (구름 마찰력) 에 대한 이야기가 좀 더 나오는데 운동 자체를 이해하기 위해 직접적으로 필요한건 아니어서 여기서는 패스하기로..
궁금한 사람은 10.9 섹션의 뒷부분을 보면 된다.
이렇게 10장 고정된 축에 대한 강체의 회전 에 대한 이야기가 끝났다. 강체라는 이상적인 개념을 도입하는 이유, 관성모멘트, 토크, 회전축, 질량중심, 굴러가는 운동의 이해 에 관한 내용이었다.
다음엔 11장 각운동량 에 대한 이야기를 시작해보자.
[참고문헌]
주 교재 : Physics for Scientists and Engineers, 9th Edition, Serway/Jewett
'일반물리' 카테고리의 다른 글
| [051-11-02] 역학 : 비고립계의 각운동량 - Angular Momentum of Nonisolated System (2) | 2022.03.10 |
|---|---|
| [050-11-01] 역학 : 각운동량 - Angular Momentum (0) | 2022.03.03 |
| [048-10-08] 역학 : 에너지 관점으로 보는 회전운동 - Energy Considerations in Rotational Motion (0) | 2022.01.03 |
| [047-10-07] 역학 : 회전운동에너지 - Rotational Kinetic Energy (0) | 2021.12.17 |
| [046-10-06] 역학 : 관성모멘트의 계산 - Calculation of Moments of Inertia (0) | 2021.12.16 |