물체의 위치가 변하는 병진운동에 대한 이야기를 전개하면서 우리는
운동 자체를 정의하고, 운동의 변화와 변화의 원인을 얘기하면서 힘을 도입했고, 힘의 작용과 가속도의 관계를 이야기하면서 뉴턴법칙에 대한 이야기를 했고, 그 후에 에너지를 도입해서 기술하는 과정을 거쳤는데,
이와 같은 과정으로 회전운동을 다루는 중 이다. 그래서 이번엔 회전 운동의 에너지에 대한 이야기를 할 차례.
회전운동은 기본적으로 회전축에 대한 운동이기 때문에 병진운동에서와 같은 “물체의 공간적 이동” 자체가 발생하지 않는다. 하지만, 물체를 이루는 각 부분은 정해진 궤도를 따라 “움직이긴” 하니까 이와 관련된 운동에너지가 있을것이라는 생각은 해 볼 수 있다.
그래서 이번에도 아래 그림과 같은 상황을 설정하고 시작할건데,
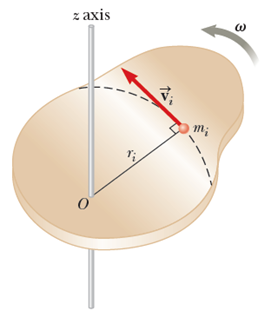
이제 그림을 보면 어떤 상황인지는 서로 알 수 있을 테니까 본론으로 바로 가자.
질량 mi 를 갖는 물체의 일부분은 다음의 선형 운동에너지를 가질것으로 생각되는데,
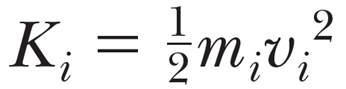
물체를 이루고 있는 모든 부분은 동일한 각속도를 가지므로, 각 부분의 접선방향 속도는 회전축으로부터의 거리에 따라 다음의 선속도를 갖는다.
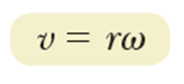
이 관계는 아래의 과정으로 얻었었다.

토크와 마찬가지로 회전하는 물체 전체의 운동에너지는 각 부분이 갖는 운동에너지를 모두 더해서 구할 수 있을텐데,

물체를 구성하는 모든 부분의 각속도 오메가는 일정하니까 위 식의 시그마 부분은 다음으로 묶어볼 수 있다.

짠.
괄호안에 들어있는게 토크 이야기에서 봤던 친구다. 관성모멘트.
그럼 우리는 저 복잡한 식을 아래와 같이 간단한 형태로 바꿔 쓸 수 있다.

앞서 이야기에서 잠깐 언급했던 것 처럼 회전운동의 기술은 물체의 관성모멘트를 구하는게 거의 전부라고 해도 과언이 아니다.
위 식으로 얻어지는 값을 우리는 물체의 회전 운동 에너지 라고 부르긴 하지만, 이게 아주 새로운 형태의 에너지는 아니다.
물체를 이루는 각 부분이 갖는 운동에너지를 더한 것 뿐 이니까.
이건 단위를 생각해보면 좀 더 명확해지는데, 다음의 운동에너지는

[kg m^2 / s^2] 의 단위를 갖고, 회전 운동에너지

역시 같은 단위를 갖는다.
관성모멘트의 단위는 [kg m^2] 이고, 각속도의 단위는 [s^-1] 이니까.
물론 각속도는 [rad/s^1] 이지만, 라디안은 단위가 아니다.
그러니까, 회전운동에너지를 회전하는 물체의 운동에너지로 받아들이는것도 괜찮다.
다음은 회전운동에 대한 일과 일률 등을 알아보자.
[참고문헌]
주 교재 : Physics for Scientists and Engineers, 9th Edition, Serway/Jewett
'일반물리' 카테고리의 다른 글
| [049-10-09] 역학 : 굴러가는 운동 - Rolling Motion of a Rigid Object (0) | 2022.03.02 |
|---|---|
| [048-10-08] 역학 : 에너지 관점으로 보는 회전운동 - Energy Considerations in Rotational Motion (0) | 2022.01.03 |
| [046-10-06] 역학 : 관성모멘트의 계산 - Calculation of Moments of Inertia (0) | 2021.12.16 |
| [045-10-05] 역학 : 토크가 작용하는 물체의 해석 - Analysis Model: Rigid Object Under a Net Torque (0) | 2021.12.16 |
| [044-10-04] 역학 : 토크 - Torque (0) | 2021.12.14 |