앞에서 우리는 회전하는 물체의 운동에너지에 대한 이야기를 했는데, 병진운동에서 그랬듯 회전운동도 에너지의 관점으로 접근하고 이해하는게 유익하지 않을까 하는 생각을 해볼 수 있다.
역시 병진운동을 다룰때와 동일하게 물체에 작용하는 토크와 그 결과로 발생하는 회전운동 사이의 관계를 일률(power) 과 일-에너지 정리의 관점으로 다시한번 들여다보자는 이야기.

위 그림과 같이 물체의 한 점 P 에 힘 F 가 작용해서 점 O 를 중심으로 물체가 회전하는 상황에 대해 생각해보자.
물체는 당연히 회전을 할 테니까 P 가 움직이는 경로는 원 일 테지만, 그 경로의 아주 짧은구간 (무한소, infinitesimal) ds 는 직선으로 간주 할 수 있을거다.
그러면 물체를 ds 만큼 회전시키기 위해 힘이 한 일은

작용한 힘의 수직방향성분만 회전운동에 영향을 주니까 sin 이 생겼다.
힘 F 에 의해 P 에 발생하는 토크의 크기는 다음과 같으므로,

일에 대한 위 식은 다음의 형태가 된다.

힘 F 가 dW 만큼의 일을 시간간격 dt 동안 했다면, 일과 시간의 비율은
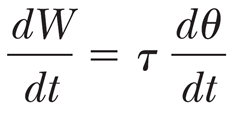
이 식의 좌변은 일률 (P, power) 이고, 우변의 미분은 각속도가 되므로, 회전운동의 일률은 다음으로 쓸 수 있다.

위 식들은 병진운동에서의 일 (dW=Fx dx) 을 다뤘던것과 완전히 같은 방식의 접근이며, 직교 좌표에서의 좌표 표현이 각도로 바뀌는 차이만 있다.
병진운동에서 에너지 도입은 현상을 “계 (system)” 의 입장에서 분석하는게 용이하도록 해줬었는데, 이는 회전운동에서도 이와 같은 접근이 가능하지 않을까 라는 가능성을 시사한다.
회전운동을 에너지 (또는 일) 의 입장에서 쓰면 어떻게 되는지 알아보자는 말.
물체에 작용하는 전체 토크는 물체의 관성모멘트와 각가속도의 곱으로 쓸 수 있음은 확인했고, 여기에 미분의 연쇄규칙 (chain rule) 을 적용하면 다음의 과정을 확인 할 수 있다.

첫 항과 마지막 항 두 개만 놓고, 다음의 관계를 이용하면,
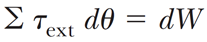
위 식은

이제 적분만 한번 하면, 외력이 회전하는 계에 한 일의 크기를 다음으로 구할 수 있다.

적분구간이 각속도여서 약간 당황 할 수도 있을텐데, 당연히 각도로 쓰는 표현으로 바꾸는게 가능하다.
위 관계는 회전운동에서의 일-운동에너지 정리 이고, 병진운동에서의 일-운동에너지 정리와 정확히 같은 입지를 갖는다.
쓸데가 많다는 말 이지.
교재에는 회전 축에 대해 대칭인 형태를 가져야 한다는 중요한 이야기가 있지만, 우리는 여기서
“회전운동은 병진운동과 똑같다고 해도 과언이 아닐만큼 같은 방식으로 기술이 가능하고,
회전운동의 토크는 병진운동의 힘과 같은 역할을 하고,
병진운동의 기술에서 질량의 역할을 회전운동은 관성모멘트가 하는구나”
정도를 잘 이해하고 넘어가도 충분하리라 생각한다.
여기까지를 알게 되면, F=ma 만큼 막강한 회전운동을 기술 할 수 있는 도구를 얻게 된 거다.
마지막으로 병진운동과 회전운동 사이의 수식적인 대칭(?) 을 확인해보고 넘어가자.

교재의 표10.3 뒤에는 부가적인 설명이 반 페이지 정도 있으니 관심있으신 분들은 찾아 보시길.
다음은 바퀴가 굴러가는 것 같은 회전운동에 대한 이야기를 하기로 하자.
[참고문헌]
주 교재 : Physics for Scientists and Engineers, 9th Edition, Serway/Jewett
'일반물리' 카테고리의 다른 글
| [050-11-01] 역학 : 각운동량 - Angular Momentum (0) | 2022.03.03 |
|---|---|
| [049-10-09] 역학 : 굴러가는 운동 - Rolling Motion of a Rigid Object (0) | 2022.03.02 |
| [047-10-07] 역학 : 회전운동에너지 - Rotational Kinetic Energy (0) | 2021.12.17 |
| [046-10-06] 역학 : 관성모멘트의 계산 - Calculation of Moments of Inertia (0) | 2021.12.16 |
| [045-10-05] 역학 : 토크가 작용하는 물체의 해석 - Analysis Model: Rigid Object Under a Net Torque (0) | 2021.12.16 |