[008] 앞의 글에 이어 물리적으로 아주 중요한, 그리고 운동량과 같이 보존되는 개념인 에너지는 상대론적 관점에서 어떻게 표현되는지 알아 볼 차례다.
이전 글에서 새로 정의한 상대론적 힘, 일(work) 에 대한 고전물리의 정의, 사칙연산보다 약간 어려운 수학 정도를 이용해서, 드디어 그 유명한 질량-에너지 등가원리 : E=mc^2 를 확인해보자.
[008-01] 힘이 한 일의 상대론적 표현
이전 논의에서 선 운동량이 상대론의 가정 : 모든 관성계에서 물리법칙은 동일해야 한다. 에 부합하려면 일반적인 형태로 다시 기술되어야 함을 확인했다. 이는 운동에너지 역시 새로운 형태로 수정되어야함을 의미한다.
정지 상태의 물체에 힘이 작용하면, 운동량의 변화가 생기고, 물체의 속력은 작용한 힘에 비례하여 임의의 값 (u) 까지 커질텐데, 이때 물체에 작용한 힘이 한 일의 정의에서 이야기를 시작해보자. (일-운동 에너지 정리)
물체에 작용한 힘이 한 일은 아래와 같다.
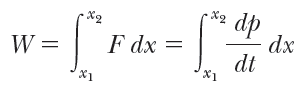
상황을 좀 간단히 보기위해 작용하는 힘과 운동방향이 모두 x 방향 이라고 가정했고, 위식은 F 의 힘이 물체를 처음위치 x1 에서 나중위치 x2 까지 이동시켰다 라는 말이다.
앞에서 새로 정의한 상대론적 운동량을 대입하여 위 식을 물체의 최종속도 : u 에 대한 식으로 바꿔보자.


위 관계를 W 의 식에 대입하고, dx=udt 로 바꿔주면 아래를 얻는다.

위 과정은 운동량이 u 에 대한 함수여서 x 에 대한 적분이 안되니, x 를 u 에 대한 식으로 바꿔준 것으로 생각하면 좀 받아들이기 편하고, 속도 u 로 시간 dt 만큼 움직인 이동거리는 dx 니까 dx=udt 로 쓸 수 있음을 생각하면 받아들이기 좀 더 쉽다.
그리고, 적분변수가 x ->t -> u 로 바뀌면서 적분 구간도 함께 변했다.
이제 위 적분의 결과로 다음을 얻는다.
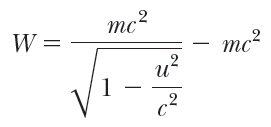
아직 잘 모르겠지만, 힘이 한 일을 구했더니 mc^2 이 나타났다!
[008-02] 상대론적 운동에너지
자, 어렸을때 졸면서 배운걸 떠올리면서 한번 생각해보자.
정지상태의 어떤 물체에 힘이 가해져서 속도를 가지고 움직이게 됐다면, 그 힘이 한 일은 온전히 물체의 운동에너지로 변환 된다. 이 말을 식으로 쓰면,

Ki 는 힘이 가해지기 전 물체의 운동에너지인데, 정지상태였으니 0 이다.
우리도 이야기의 시작에서 정지상태의 물체에 가해지는 힘을 다루는것으로 약속했으니, 앞에서 계산해둔 상대론적 일은 모두 물체의 운동에너지로 변환됐음을 알 수 있다. 이를 상대론적 운동에너지라 하고, 식으로 쓰면 아래와 같다.

이전 글에서와 마찬가지로, 정지상태의 물체와 동일한 계에 속한 사람이 관측하는 물체의 속도이기 때문에 u 로 표기했고, 이제 여러번 본 감마 가 다시 등장했다.
물론 위 식은 고에너지 입자 가속 실험에서 충분히 검증 되었다.
[008-03] 운동에너지의 상대론적, 고전적 표현 비교
이제 약간 익숙치 않은 수학을 가져다 쓸건데, 궁금한사람은 이항정리를 찾아보면 된다.
물체의 속도가 빛의 속력보다 아주 느린경우, u/c <1 이 되므로, 감마는 아래와 같이 계산된다.

위 식의 빨간 네모의 계산에서 이항정리를 이용하는데, 간략한 내용은

루트 안의 u/c 를 베타로 치환하면 위와 같이 베타의 거듭제곱의 형태로 쓸 수 있고, 이미 베타는 1보다 아주 많이 작으므로 베타를 거듭제곱 할 수록 그 값은 점점 더 0 에 가까워지므로, 계산 결과를 1 과 첫번째 항의 합으로 취급해도 차이가 없다는 것 이다.
이 내용을 상대론적 운동에너지의 식에 대입하면,

이 되어, 우리가 알고있는 고전물리의 운동에너지와 동일한 형태가 된다.
다음 그래프로 두 표현의 차이를 확인해보자.

빨간색은 상대론적 표현, 파란색은 고전적 표현의 그래프인데, 빨간색 그래프의 경우, 감마 때문에 물체의 운동에너지가 증가해도 속도는 빛의 속력에 도달하지 못하고 수렴하는 형태를 볼 수 있다.
하지만, 파란색 그래프는 물체가 큰 운동에너지를 갖는 조건에서 물체의 속도가 빛의 속력 이상으로 계속 증가함을 볼 수 있다. 고전적 표현으로는 빠른 속도의 물체에 대한 해석이 불가능하다는 의미.
물론 느린속도에서는 두 그래프가 겹쳐지므로, 동일한 결과를 얻게된다. (빛의 속력의 10%, 0.1c 는 30,000,000 m/s 이고, 음속은 340 m/s 이다.)
[008-04] 질량-에너지 등가
여기까지 이야기를 잠시 정리해보자.
1. 모든 관성계에서 물리법칙이 동일해야 함을 운동량 보존에 적용해서 운동량 p 에 대한 상대론적 정의를 했고, 이를 이용해 힘의 상대론적 표현을 확인했다.
2. 위 힘을 이용해 힘이 한 일의 상대론적 표현을 알아봤고, 정지상태의 물체에 힘이 작용하는 경우 (움직이고 있는 물체여도 관계없다) 를 고려하여, 힘이 한 일과 물체의 운동에너지 사이의 관계를 알아봤다. 감마가 등장했다.
3. 운동에너지의 상대론적 표현은, 물체의 속도가 빛의 속력에 비해 아주 느릴때는 고전물리와 동일한 방식으로 현상을 기술하고, 물체의 속도는 빛의 속도에 도달하지 못한다는 의미를 모두 포함한다.
자, 이제 위에서 구한 운동에너지를 다시한번 불러오자.

위 식의 mc^2 은 물체의 속력에 관계 없는 값 인데, (물체의 속력에 의한 변화는 감마가 모두 책임진다) 이를 물체의 정지 에너지 (Rest Energy) 라 한다.

이게 바로, 그냥 대충 거의 모든 사람이 알고있는 질량-에너지 등가 원리이며, 질량 자체가 에너지임을 의미한다.
다른말로 하면, 빛의 속력은 엄청 큰 숫자인데, 그걸 제곱하면 더욱 더 큰 숫자가 될테니, 질량이 아주 작은 물체여도 존재 자체가 갖는 에너지는 어마어마 하다는 의미이고, 현재 핵물리와 입자물리의 기본개념으로 열심히 활동 중 이다.
위 운동에너지의 식은 정지에너지에 감마가 곱해진 항을 갖고있는데, 이는 물체의 속력에 영향을 받는 값이며, 물체의 전체 에너지 (Total Energy : E) 라 한다.
물체의 전체 에너지는 물체의 운동에너지와 정지에너지의 합 이며,

전개한 운동에너지 식에서 다음과 같이 구할 수 있다.

물체의 전체 에너지는 다음과 같다.

[008-05] 중요하지만 부수적인 이야기
1. 입자의 전체 에너지와 상대론적 운동량을 이용하면 다음을 얻을 수 있는데,

정지 상태의 입자는 운동량 p=0 이므로, 전체 에너지는 정지에너지와 같으며 E=ER=mc^2 이 된다.
2. 광자 (Photon) 는 질량을 갖지 않으므로, 위 식의 m=0 이 되어 에너지 E=pc 가 된다. 이 표현은 진공에서 빛의 속도로 움직이는 광자의 에너지와 운동량에 대한 정확한 상대론적 표현이다.
3. 질량 m 은 입자의 운동상태 (속력) 와 무관하므로 모든 계의 관찰자가 보기에 동일한 값을 갖는다. 그래서 m 을 불변질량 (invariant mass) 으로 부르기도 한다.
4. 아원자입자 (subatomic particles) 를 다루는 경우, 입자의 에너지 단위를 전자볼트 (eV : electron volt) 로 쓰는데, 이는 하나의 전자가 1V 의 전위차에 놓였을때 전자가 갖는 에너지 이며, 익숙한 단위 (J) 로의 변환은 다음의 관계를 이용해서 할 수 있다.

[008-06] 요약
1. 운동량에 대한 상대론적 정의와 일-운동에너지 정리를 이용해 질량-에너지 등가원리를 확인했다.
2. 질량-에너지 등가원리는 질량 자체가 에너지를 갖는다는 의미이다.
3. 모든 물리량에 대한 상대론적 표현은 빛의 속력에 비해 아주 느린 속도에서 고전물리와 동일한 방식으로 현상을 기술한다.
4. 아주 큰 속도에서의 상대론적 효과는 운동량과 에너지에는 영향을 미치지만, 질량에는 영향을 주지 않으며, 이런 이유로 질량을 불변질량 (invariant mass) 으로 부른다.
특수상대론에 대한 이야기는 [002] 부터 [008] 까지 이고, 다음은 일반상대론에 대한 이야기를 해보자.
[참고문헌]
주 교재 : Physics for Scientists and Engineers, 9th Edition, Serway/Jewett
'일반물리' 카테고리의 다른 글
| [010-01] 양자물리학의 시작 - Quantum Physics (2) | 2020.03.03 |
|---|---|
| [009] 일반 상대성 이론 - 상대론 마지막 글 (0) | 2020.02.29 |
| [007] 상대론적 운동량 (0) | 2020.02.12 |
| [006] 로렌츠 속도 변환 - The Lorentz velocity transformation equation (0) | 2020.02.11 |
| [005] 로렌츠 변환 - The Lorentz Transformation Equations (0) | 2020.02.10 |