이제 전류에 대한 이야기를 볼 차례이고, 회로이론 (이론 이라기엔 쓸데없이 거창한데..) 의 시작이고, 나아가 자기장의 근원에 대한 이야기이기도 하다.
뭐.. 드럽게 그럴싸 하게 썼네..
항상 강조하지만, 무엇을 어떻게 정의하고 있는지를 잘 아는게 물리 뿐만 아니라 모든 공부의 시작이자 끝 이라 생각한다.
어떤 물질을 통과하는 전하의 흐름을 상상해보자. 이 때 흘러간 양은 첫째, 전하가 “어떤 물질”을 통과 했는가와 둘째, 물체의 양단간에 걸려있는 “전위차” 두 가지에 영향을 받는다.
그리고, 뭐가 어찌됐든, 양이 많든 적든, 전하의 순 흐름 (net flow of charge) 이 있으면 전류가 존재한다고 표현한다.
여기까지만 봐도 우리가 평소에 사용하는 “전류가 흐른다” 는 말이 좀 이상하다는 생각이 든다.
전류가 흐르는게 아니라 실제로 흐르는건 전하다.
이제 전류를 정량적으로 정의해보자.
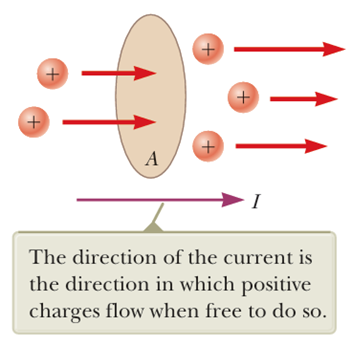
그 첫 단계는 위 그림과 같이 전하가 임의의 단면을 수직으로 통과한다는 가정을 해야한다.
저 단면은 전하가 이동하는 도선의 단면으로 생각해도 좋다.
전류는 이 단면을 통과하는 전하량의 비율로 정의하고,
** 양전하의 이동 방향과 전류의 방향이 같음을 잘 봐두자.
임의의 시간 간격 Δt 동안 이 면을 통과한 전하량이 ΔQ 라면, 평균 전류 (average current) 는 단위 시간동안 면적 A 를 통과한 전하량이 된다.
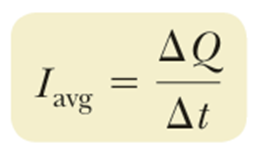
여기에 Δt 를 0으로 보내는 극한을 취해 순간전류 (instantaneous current) 를 구할 수 있고, 우리가 보통 “전류”라 부르는 전하의 흐름은 순간전류를 의미한다.
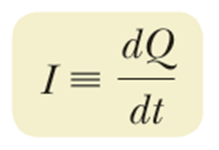
SI 단위계에서 전류는 암페어 (A. ampere) 를 단위로 쓴다.
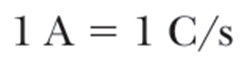
즉, 1암페어의 전류는 우리가 관심있는 단면을 1초동안 1C의 전하량이 지나는 경우를 의미한다.
양이나 음으로 대전된 입자가 이동 할 수 있을텐데, 물론 둘 다 일수도 있고,
우리는 처음부터 양전하의 이동방향을 전류의 방향으로 약속해서 사용하기로 했다.
근데, 구리와 같은 도체의 경우 전류는 대부분 음전하를 갖는 전자의 움직임에 의해 발생하기 때문에 일반적인 도체에 발생하는 전류는 전자의 이동 방향과 반대 방향을 갖는다.
배터리와 같이 양/음 전하를 갖는 물질이 동시에 작용해서 전류가 발생하는 경우, 전하를 띄고 움직이는 물질을 전하 운반체 (charge carrier) 라고 부른다.
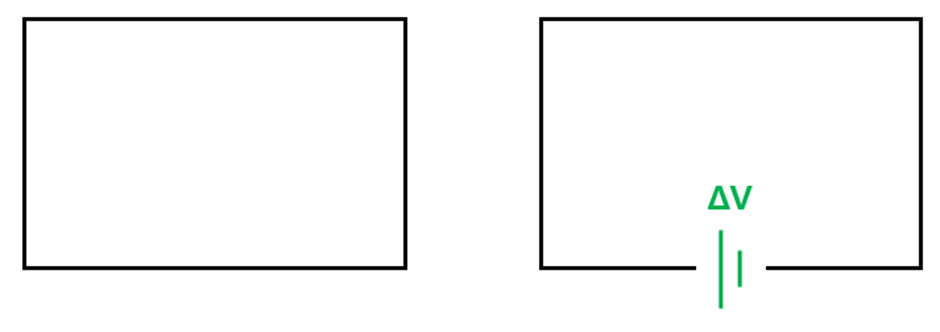
위 그림의 왼쪽과 같이 도선만으로 회로를 만들면 도선의 모든 지점에서 전위가 같기 때문에 전기장이 존재하지 않고, 따라서 전류도 발생하지 않지만,
오른쪽처럼 회로에 전지를 연결하면 도선의 양 끝단 사이에 전위차가 발생하고, 이에 의해 도선에는 전기장이 발생하고, 이 전기장은 도선의 전자를 움직여 전류를 발생 시킨다.
전하의 흐름은 우리 눈에 보이지 않기 때문에 실제 상황에 적용 가능한 모델을 만들어 취급 할 필요가 있는데, 이걸 알아보자.
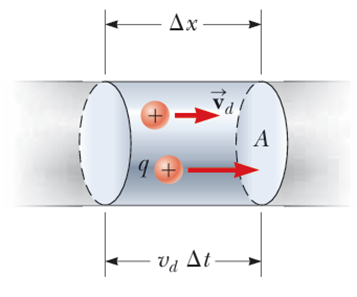
위 그림과 같이 A 의 단면적을 갖는 원통형 도선의 전류를 생각해보자.
단위 부피당 전하 운반체 (charge carrier) 의 개수 즉, 전하 운반체의 밀도를 n 이라 하면, 위 그림에 표시된 영역에 들어있는 전체 전하량은 다음과 같고, q 는 전하 운반체 하나의 전하량이다.
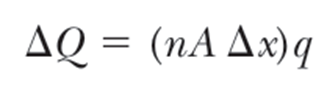
원기둥의 부피에 밀도를 곱하고 전하 운반체 당 전하량을 곱한 것.
근데 우리는 전류를 전하량과 시간의 비율로 정의 했으니까 위 식이 시간에 대한 항을 포함하도록 변형 할 필요가 있다.
그래서 도입하는게 전하 운반체가 도선을 따라 이동하는 속도이고, 이걸 이용해 위의 식을 다시 쓰면,
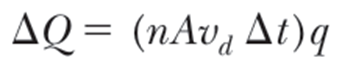
이 식의 양변을 Δt 로 나누면 앞에서 잠깐 나온 평균 전류를 구할 수 있고, 좀 더 현실적인 개념을 포함하는 식이 된다.
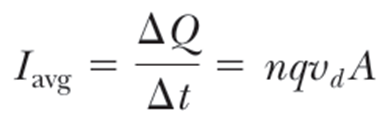
이 식이 가장 현실적이고 실제로 사용 가능한 전류에 대한 식 이라고 알고 있어도 큰 문제는 없고, 위 식의 캐리어 (이 표현이 편해서 그냥 이렇게 써야겠다) 의 속력은 표류속도 (drift speed) 라 부르는 평균속도를 의미한다.
마지막으로 표류속도라는 개념을 쓰는 이유를 알아보자.
도선 안의 전자가 전기장에 의해 이동 할 때는, 물론 전기장이 없을 때도 마찬가지겠지만,
도선 내부의 금속 원자들이나 다른 전자들과 계속해서 충돌하면서 움직이게 된다.
마치 아래 그림처럼.
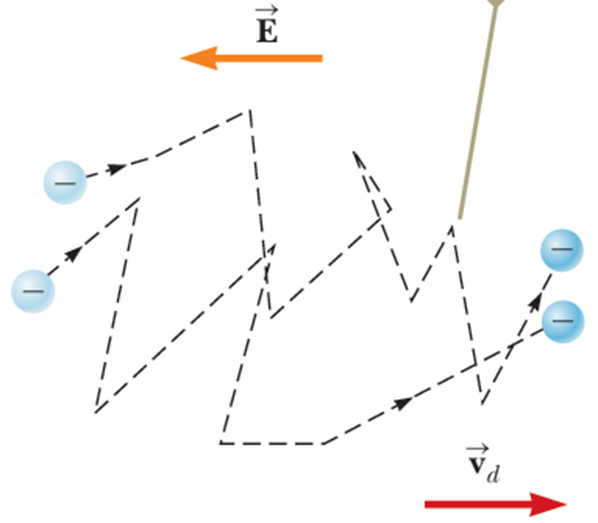
이렇게 실제로 전자가 충돌하며 이동하는 과정을 포함한 이동 속도를 표류속도 라는 이름으로 도입해서 적용한 것 이다.
그리고 실제로 전자의 이동속도는 생각보다 상당히 느리다.
여기까지.
[참고문헌]
주 교재 : Physics for Scientists and Engineers, 9th Edition, Serway/Jewett
'일반물리' 카테고리의 다른 글
| [093-27-02] 저항 - Resistance (0) | 2024.06.14 |
|---|---|
| [092-27-01-01] 전자의 표류 속도 - Drift speed of Electrons (0) | 2024.06.13 |
| [090-26-08] 문제풀이 (0) | 2024.06.11 |
| [089-26-07] 유전체의 원자적 기술 – An Atomic Description of Dielectrics (0) | 2024.06.10 |
| [088-26-06] 전기장 속의 전기 쌍극자 – Electric Dipole in an Electric Field (0) | 2024.06.05 |