[090-26-08] 문제풀이

<예제 26.7>

금속판의 간격 d, 면적 A 인 평행판 커패시터의 가운데에 두께 a 인 대전되지 않은 금속판을 추가했을 때,

(A) 가운데 금속판을 포함하는 커패시터의 전기용량은?

(B) 가운데 금속판이 무한히 얇으면 원래 커패시터의 정전용량에 영향을 주지 않음을 보여라.

 

풀이)

(A) 도체는 유전체와 달리 커패시터의 금속판에 축적되는 전하량과 동일한 전하량으로 대전되고, 그 유효 전하들은 도체의 양쪽 표면에 분포하게 될 테니, 우리는 이 문제를 아래 그림과 같이 직렬 연결된 두 개의 커패시터로 취급해서 다룰 수 있다.

 

 

도체의 특징에 관해서는 이전에 다뤘던 적이 있다.

 

https://physicslog.tistory.com/entry/075-24-04-%EC%A0%84%EC%9E%90%EA%B8%B0%ED%95%99-%EC%A0%95%EC%A0%84%EA%B8%B0-%ED%8F%89%ED%98%95-%EC%83%81%ED%83%9C%EC%9D%98-%EB%8F%84%EC%B2%B4-Conductors-in-Electrostatic-Equilibrium

[075-24-04] 전자기학 : 정전기 평형 상태의 도체 - Conductors in Electrostatic Equilibrium

 

직렬 연결된 커패시터의 총 커패시턴스는 아래의 과정으로 구할 수 있다.

 

 

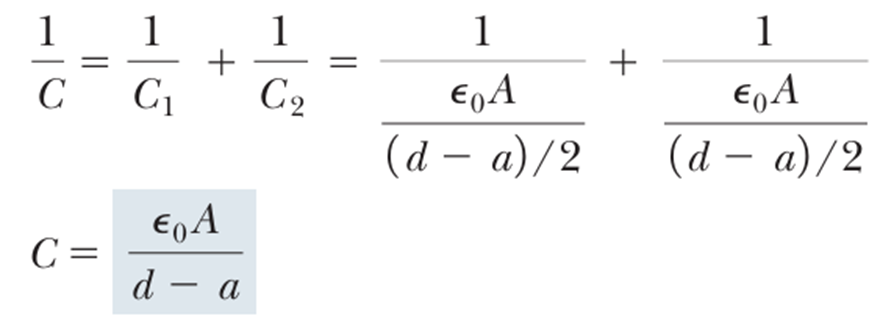
계산이 어려운건 아니니까 여기까지.

 

 

(B) 위 결과에 금속판의 두께 a 가 0으로 가는 극한을 취하면,

 

 

무한히 얇은 도체판을 커패시터에 추가해도 원래 커패시터의 전기용량에는 영향을 미치지 않는다.

 

 

 

<예제 26.8>

아래 그림과 같이 간격 d, 전기용량 C0 를 갖는 커패시터에 유전상수 κ, 두께 fd 를 갖는 유전체를 넣으면 전기용량이 어떻게 달라지나?

 

 

풀이)

우린 예제 26.7 에서 무한히 얇은 금속판은 커패시터의 전기용량에 영향을 주지 않는다는걸 확인했다.

이번 문제에 이 사실을 적용하기 위해 유전체의 아랫면에 무한히 얇은 금속판을 추가했다고 생각해보자.

그러면 문제는 앞에서와 마찬가지로 유전체가 있고, 없는 두 개의 커패시터가 직렬연결된 형태로 바꿔서 다룰 수 있게 된다.

이제 계산은 간단하지.

 

 

위 결과에 f 가 1을 향해가는 극한을 취하면 커패시터의 공간 전체가 유전체로 채워진 경우와 같은 결과를 주고,

f가 0을 향해 가는 극한을 취했을 때, 커패시터의 공간에 아무것도 채워지지 않았을 때와 같은 결과를 주는 것을 확인 할 수 있으므로, 이를 통해 간접적으로 올바른 관계식을 얻었다는것을 확인 할 수 있다.

 

물리 문제들은 평소에 그냥 막 계산부터 하기 보다는 문제를 어떻게 보고 접근 할 것인가를 생각 해 보는게 많은 도움이 된다.

 

교재 중간중간에 있는 예제들의 풀이는 모두 어떻게 주어진 상황을 이해하고 접근 할 것인가를 자세히 설명하고 있으니, 가능하면 한번씩 읽어보길 바란다.

 

 

 

[참고문헌]
주 교재 : Physics for Scientists and Engineers, 9th Edition, Serway/Jewett