[076-25-01] 전자기학 : 전위와 전위차 - Electric Potential and Potential Difference
이제 전위 (electric potential) 에 대한 이야기를 할 차례인데, 전기와 자기 얘기는 이해하기가 참 어려운 부분이라 앞서 글 처럼 손 그림 같은걸 좀 넣을 생각이다. 집사람한테 아이패드 프로를 선물
physicslog.tistory.com
우린 위의 글에서 전기장이 형성되어 있는 공간의 임의의 두 지점 사이 전위차를 다음으로 정의 했다.

이는,
공간에 형성되어 있는 전기장을 정확히 알면, 원하는 두 지점 사이의 전위차를 구할 수 있다는 얘기였고,
물론 이전 글에서 시작점을 아주아주 먼 곳으로 설정해서 원하는 한 지점의 전위를 구하는것도 가능하다는걸 확인했다.
[078-25-03] 전자기학 : 점전하에 의한 전위와 포텐셜 에너지 - Electric Potential and Potential Energy Due to Po
그림과 함께 시작. 이제 우리는 양전하 q 가 그 주변 공간에 전하 q 로부터 멀어지는 방향을 갖는 전기장을 형성한다는 것을 알고있다. 이번엔 원천전하 q 로부터 r 만큼 떨어진 위치의 전위가 어
physicslog.tistory.com
이번에는 이와 반대로 알고 있는 특정 영역의 전위를 가지고 전기장을 구할 수 있는지 알아보자
위 식에서 아주 짧은 거리 ds 만큼 떨어져 있는 두 지점의 전위차 dV 는 적분기호를 생략하고 다음으로 구할 수 있다.

쉬운 이해를 위해 공간을 x축 하나로 제한하면 우변의 내적은 다음이 된다.
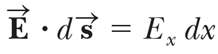
그럼 다음을 얻을 수 있다.
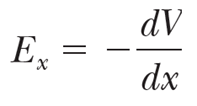
전위를 공간에 대해 미분한 결과에 음수를 취하면 전기장을 얻을 수 있다.
이 말을 약간 수학적인 표현으로 바꾸면,
전기장은 위치에 대한 전위의 변화율을 측정한 것 이다.
라고 할 수 있고, 이를 교재에서는 다음으로 쓰고 있다.
The electric field is a measure of the rate of change of the electric potential with respect to position.
… 당연히 여기까지 읽어도 어려울 수 있으니까, 마지막으로
좀 익숙한 위치와 속도의 관계와 전위와 전기장의 관계를 비교해보면,

변화량과 미분에 대한 이야기는 아래 글을 읽어보자.
[005-02] 기울기. 극한. 미분과 상상력.
[005-02-00] 원래는 이 얘기를 쓸려고 시작한건데, 쓰다보니 길어져서 두 편으로 나눴다. 앞에서는 숫자에 대한 이야기를 했고, 이제 미분과 적분에 대한 이야기를 해보자. 미분과 적분이 어려운 이
physicslog.tistory.com
등전위면과 전기장의 관계를 생각해보자.
등전위면을 따라 ds 만큼 위치가 변한 경우, 이 운동에서 전위의 변화량 dV=0 이다.
말 그대로 전위가 동일한 면을 따라 움직였으니까.
그러면 아래 관계에 따라

두 벡터 E 와 ds 의 내적은 0 이 되는데, ds 는 등전위면을 따라 움직인 과정을 의미하니까, 자연스럽게, 전기장 벡터 E 는 등전위면 벡터 ds 에 수직이 되어야 한다.
이 설명이 다양한 상황에 적용되면 아래의 전기장 선과 등전위면 을 얻을 수 있다.

위 두번째 그림과 같이
주어진 전하분포에 의한 전기장이 구 대칭성을 갖고 있어서 동경 방향 (radial) 의 변화만 존재한다면, 우리는 다음의 관계로 전위와 전기장을 다룰 수 있다.

언젠가 얘기했던,
이런 다양한 좌표계를 왜 사용하느냐면,
동경방향의 변화만 갖는 전기장의 경우, 전위는 다음의 형태 일 테고,

이에 대한 전기장은 위 전위를 r 에 대해 미분하고 음을 취한 다음의 형태가 된다.

물론 일반적인 3차원 좌표계에서 전위는 세 성분을 갖는 V(x, y, z) 의 형태이고, 각 성분에 대한 전기장은 전위의 편미분으로 구할 수 있다.

여기까지.
[참고문헌]
주 교재 : Physics for Scientists and Engineers, 9th Edition, Serway/Jewett