
이번에는 금속에서의 전기 전도를 설명하기 위한 모델을 알아 볼텐데, 사진속의 사람이 1900년에 처음 제안한 모델이다.
이 모델에 따른 전기 전도의 해석은 옴의 법칙과 이어지고, 금속에서 전자의 움직임과 비저항이 관련 있음을 보여주기도 한다.
아래 글에서 막스 플랑크가 흑체 복사 이론의 설명을 위해 물리적 구성 요소와 그 요소의 거동에 대한 모델을 만들었듯,
모든 이론은 “왠지 전도도가 높으면 전자가 잘 움직일거 같잖아?” 와 같은 방식으로 만들어지지 않는다는 것을 다시 한번 생각해봤으면 좋겠다.
[010-01] 양자물리학의 시작 - Quantum Physics
[010] 이제 현대물리의 근간을 이루는 두 이론 - 상대성 이론, 양자물리학 - 중 양자물리학에 대한 이야기를 해보자. 빛의 속도에 견줄 수 있을만큼 아주 빠른 속도로 움직이는 입자를 다루려면,
physicslog.tistory.com
여기서도 마찬가지로, 전기 전도를 지금의 방식으로 취급하는 것이 얼마나 정교한 설명과 이해를 바탕으로 하는지 알아보자.
1. 물리적 구성요소 (Physical components)
도체를 규칙적인 원자의 배열과 자유 전자 (free electrons, conduction electrons) 의 조합으로 취급한다.
고체의 일부가 아닌 상태의 원자인 경우 전자는 원자에 속박되어 있지만, 원자가 모여 고체를 이루면 자유 전자의 특성을 갖고 움직인다.
2. 구성 요소의 동작 (Behavior of the components)
(a) 전기장이 인가되지 않은 경우, 도체 내부의 전자는 아래 그림과 같이 무작위의 방향으로 움직인다.

이건 통에 담긴 기체 분자의 무작위적 움직임과 같이 이해해도 좋고, 실제로 어떤 과학자들은 전자 가스 (electron gas) 로 금속 내부의 전자를 취급하기도 한다.
(b) 이제 이 계에 전기장이 인가되면, 아래 그림과 같이 전자들은 전기장의 반대 방향으로 슬슬 움직일텐데, 이 때 움직이는 속도는 앞서 계산한 바와 같이 0.1 mm/s 수준이다.
물론, 다른 입자와 상호작용 없이 홀로 움직이는 전자의 속도는 10^6 m/s 로 엄청나게 빠르지만, 도체 안에는 엄청난 수의 금속 원자와 다른 자유전자들이 있고, 우리가 관심을 갖고 있는 전자는 이 입자들과 끊임없이 충돌하면서 움직이기 때문에 속도가 느려진다.

(c) 원자와의 충돌 후 전자의 움직임은 충돌 전 운동과 무관하고, 인가된 전기장에 전자에 해준 일에 의해 전자가 얻은 에너지는 충돌에 의해 원자로 전달된다.
마지막에 언급한 충돌에 의한 원자로의 에너지 전달은 계의 내부에너지를 발생시키고, 이는 도체의 온도를 상승시키는 역할을 하게된다.
이제 전기장과 전자의 질량 및 전하량으로 전자의 표류속도 (vd) 를 어떻게 쓸 수 있는지 알아보자.
전기장이 인가된 질량 me, 전하량 q (-e) 를 갖는 전자는 F = qE 의 힘을 받고, 이 관계를 뉴턴의 두번째 운동 방정식과 연결하면,

인가하는 전기장이 일정하니까, 전자의 가속도는 일정 할 테니, 우리는 전자를 등가속 운동하는 입자로 취급 할 수 있다.
충돌 후 임의의 순간을 t=0 으로 삼고, 이때 전자의 속도를 vi (초기속도) 라 하면, 다음 충돌이 발생하기 이전까지 아주 짧은 시간 간격 t 이후 전자의 속도는 다음으로 쓸 수 있다.
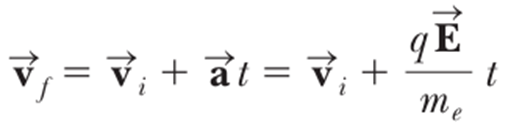
이제 도선 전체에 존재하는 모든 전자에 대한 vf 의 평균을 구해보자.
앞의 구성요소의 거동 (a) 에서, 전자의 초기 속도 vi 의 방향이 무작위라고 했으니, 모든 전자의 초기속도의 합은 반대 방향들이 상쇄에 의해 0 으로 생각 할 수 있다.
이제 충돌 과 충돌 사이의 모든 가능한 시간 간격의 평균을 τ 라 하면, 최종속도 vf 의 평균은 표류속도 vd 와 같아진다.

이제 이렇게 구한 표류속도를 앞에서 구한 평균 전류에 대입하면,

전류밀도 J 는 전류를 도선의 단면적으로 나눈 값 이니까,

이 관계를 옴의 법칙과 비교해보면, 도체의 전도도와 비저항의 표현을 구할 수 있다.

도체의 전도도와 비저항은 전기장의 세기와 관계 없고, 이는 옴의 법칙을 따르는 도체의 특성이다.
충돌 간 시간간격은 금속 원자의 크기와 전자의 밀도 (부피당 개수) 의 영향을 받을 텐데, 이건 금속원자가 크거나, 전자의 밀도가 높으면 금방 다음 충돌이 발생 하게 될 것이라는 말이고,
이는 평균 자유 행로 (mean free path) 라 부르는, 이전 충돌과 다음 충돌 사이에 평균적으로 전자가 움직일 수 있는 거리를 전자의 평균속력으로 나눈 값 이다.
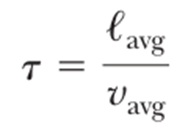
근데 아쉽게도..
이렇게 어렵게 어렵게 구한 고전 모델의 전도도와 비저항은 온도에 따른 전자의 속도를 비롯한 여러가지 변수들을 모두 포함해도 실제 값을 정확히 내어주지 못한다.
양자역학에서는 모든 물질을 파동적 성질과 입자적 성질을 모두 갖는다는 파동-입자 이중성에 대한 얘기를 하는데,
[014] 입자의 파동적 성질 - Wave Particle Duality
[014] 광전효과와 콤프턴효과는 파동이라고 생각했던 빛과 x-선을 입자라고 간주해야 설명이 가능한 현상에 대한 이야기였다. 그리고 전자기복사에 대한 이야기에서는 빛이 입자와 파동의 성질
physicslog.tistory.com
정확한 도체의 전도도와 비저항을 예측하기 위해서는 이 양자역학적 모델의 도입이 필수적이다.
도체 내부의 전자가 파동의 성질을 갖고, 금속 원자들이 주기적으로 배열되어 있다면, 전자는 원자와의 충돌 없이 말 그대로 “자유롭게” 이동 할 수 있을거다.
바다에 부표가 떠 있어도 파도는 아무 상관없이 진행 할 수 있듯이.
아주 이상적인 도체의 경우 충돌은 전혀 일어나지 않고, 전자의 평균 자유 행로는 무한대가 되어 비저항은 0 이 될거다.
도체에 불순물이 섞여 있거나, 구조적 결함이 발생해서 원자의 배열이 규칙적이지 않은 경우에만 전자의 산란이 일어날거다.
이러한 모델에서 도체의 온도가 높아지면 원자의 열적 운동이 많아지고, 원자 배열은 낮은온도에 비해 불규칙적이게 되어 전자의 평균 자유 행로는 짧아지고, 도체의 비저항은 증가하는 결과를 발생시킨다.
이 내용은 일반물리의 범위를 넘어가기 때문에 여기서 자세히 다루지는 않지만, 전자의 파동적 성질을 반영한 양자역학 모델은 실제 측정값과 잘 맞는 도체의 비저항과 온도에 따른 변화 특성을 보여준다.
여기까지.
[참고문헌]
주 교재 : Physics for Scientists and Engineers, 9th Edition, Serway/Jewett
'일반물리' 카테고리의 다른 글
| [096-27-05] 초전도체 - Superconductors (0) | 2024.09.05 |
|---|---|
| [095-27-04] 저항과 온도의 관계 - Resistance and Temperature (0) | 2024.06.21 |
| [093-27-02] 저항 - Resistance (0) | 2024.06.14 |
| [092-27-01-01] 전자의 표류 속도 - Drift speed of Electrons (0) | 2024.06.13 |
| [091-27-01] Electric Current - 전류 (2) | 2024.06.12 |