가우스 법칙에 대한 마지막 이야기로 정전기평형 상태에 있는 도체의 특징을 알아보자.
위 문장에서 어려운 단어라면, 정전기 평형 과 도체 일텐데,
좋은 도체는
물질을 구성하고 있는 원자에 구속되지 않아 물질 내부에서 이동이 자유로운 자유전자로 대표되는 전하를 갖는 물체 이다.
정전기 평형 상태는
도체 내부에 존재하는 전하의 순 운동 (net motion) 이 없는 상태 를 말하고,
그러니까 지금 우리가 알아볼려고 하는건,
도체 내부 자유전자의 순 운동이 없는 상태의 도체가 갖는 특징이 무엇인가 이다.
정전기 평형 상태의 도체가 갖는 특징 네 가지부터,
1. 도체의 속이 채워졌든 비었든 도체 내부의 전기장은 0 이다.
2. 절연된 상태의 도체가 대전되는 경우, 초과 전하는 도체의 표면에만 존재한다.
3. 대전된 도체 외부의 전기장은 도체 표면에 수직이고, 크기는 면전하밀도/유전율 이다.
4. 형태가 균일하지 않은 도체의 경우, 곡률반경이 가장 작은 위치의 면전하밀도가 가장 크다.
첫번째 특징부터 자세히 알아보자.
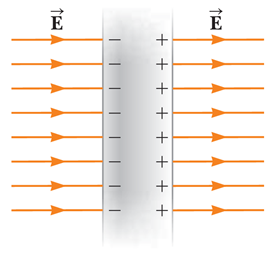
외부에서 전기장을 인가하지 않은 경우에는 당연히 도체 내부 전하들이 균일하게 분포되어 있을 텐데,
위 그림과 같이 외부에서 전기장을 인가하면, 얘기가 좀 달라진다.
외부 전기장이 인가되면,
도체 내부 전하들의 이동이 발생하게 되고,
도체 내부에는 외부에서 가해진 전기장과 크기가 같고 방향이 반대인 전기장이 발생하며,
이 두 전기장이 상쇄되어 도체 내부의 전기장은 여전히 0 으로 유지된다.
이 모든 과정은 보통의 도체에서 10^-16 초 이내에 일어나기 때문에,
그냥 항상 0 이라고 생각하는게 편하다.
그림도 그렇고.. 앞의 설명에서 전기장이 발생 한다는 말 때문에
전기장이 발생했는데 어떻게 0 이라는지 좀 이상할 수 있는데 아래 그림을 보자.
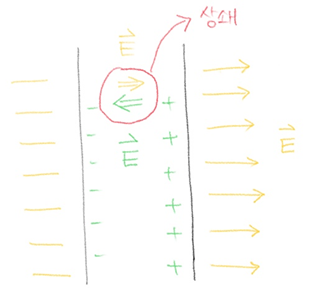
노란색 외부의 전기장을 겪고 있는 도체는 내부에도 외부의 전기장이 영향을 주는데, 이로인해 내부에 발생한 녹색의 전기장은 외부의 전기장을 상쇄하는 역할을 해서,
결국 내부의 전기장이 0 이 된다는 얘기다.
두번째 특징.
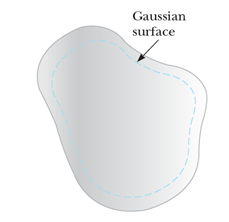
도체 내부에 가우시안 면을 설정해보자.
정전기평형 상태의 도체 내부 전기장이 0 인건 알았으니까, 설정한 가우시안 면의 모든 위치에서의 전기장 역시 0 이다.
이 말은,
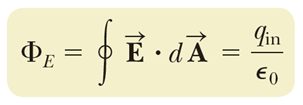
가우시안 면을 통과하는 선속이 0 이라는 것 이고, 이건 가우시안 면 내부의 순 전하 (net charge) 가 0 이라는 의미가 된다.
우리는 이 가우시안 면을 표면에 아주아주 가깝게 설정 할 수도 있을텐데,
그럼에도 불구하고 이 면은 도체의 내부에 존재하므로,
이때에도 가우시안 면 내부의 순 전하는 0이어야 하니까,
전하는 도체의 표면에만 존재한다는 결론을 얻을 수 있다.
가우스 법칙으로 표면의 전하가 어떻게 분포하고 있는지 까지는 알 수 없지만, 표면에만 존재한다는 사실은 확인 할 수 있다.
세번째 특징.
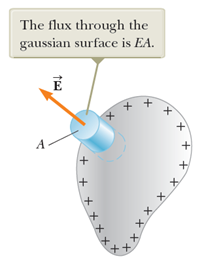
이 그림의 가우시안 면은 약간 상상을 해야하는데,
원기둥의 두 밑면 중 하나는 도체의 외부에, 하나는 도체의 내부에 있는 상태다.
전기장은 도체 표면에 수직이니까 가우시안 면의 옆면을 지나는 선속은 0.
도체 내부의 전기장이 0 이니까, 도체 안에 있는 원형의 밑면을 지나는 선속은 0.
이제 도체 밖에 있는 원형 면 하나만 남았는데,
여기에 가우스 법칙을 적용하면,
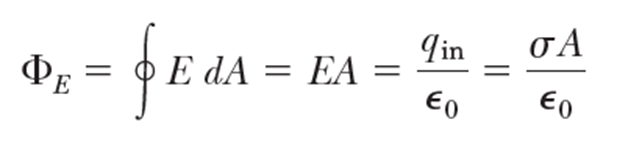
여기에 아래의 면전하밀도를 적용하면,
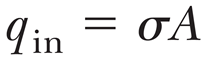
따라서 도체 외부에서 전기장의 크기는
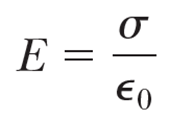
네번째 특징은 전위에 대한 얘기를 하면서 다루기로 하자.
이번에 다룬 도체의 특징은 시험을 위해서라도 꼭 알아둬야 할 내용이고,
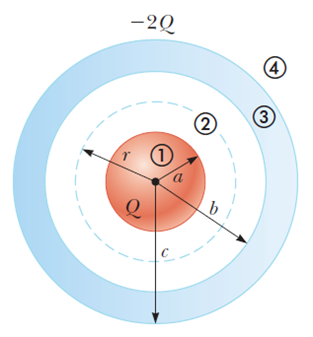
아래 그림 같은 형태를 포함하는 제일 마지막 예제는 한번쯤 봐 두면 좋다.
시험 내기가 좋아.
[참고문헌]
주 교재 : Physics for Scientists and Engineers, 9th Edition, Serway/Jewett
'일반물리' 카테고리의 다른 글
| [077-25-02] 전자기학 : 균일한 전기장 내부의 전위차 - Potential Difference in a Uniform Electric Field (0) | 2023.02.14 |
|---|---|
| [076-25-01] 전자기학 : 전위와 전위차 - Electric Potential and Potential Difference (0) | 2023.02.08 |
| [074-24-03] 전자기학 : 가우스 법칙의 응용 - Application of Gauss's Law to Various Charge Distributions (0) | 2023.02.02 |
| [073] 전자기학 : 가우스 법칙을 이해해보자. (0) | 2022.10.25 |
| [072-24-02] 전자기학 : 가우스 법칙 - Gauss's Law (0) | 2022.10.24 |