전기선속 (flux) 을 정의하면서 가우스 법칙이 다음의 형태라는 것을 알아봤고,

이제 이걸 실제로 어떻게 활용하는지 예제를 통해서 알아보자.
물론 시험에도 잘 나오는 단골 문제들 이다.
저 면적분을 어떻게 처리하느냐에 관한 얘기이고, 주어진 전하분포의 대칭성 (symmetry) 을 이용해서 저 식을 취급하기 편한 형태로 바꾸는 과정을 알아보는거다.
여기서 중요한 건 관심 있는 전하분포가 가우스 법칙을 적용 할 수 있을 만큼 충분한 대칭성을 갖느냐를 파악하는건데, 예제의 그림을 보면 그게 무슨말인지 알 수 있을거다.
가우스 법칙의 적용 순서는 다음과 같은데,
1. 가우스 법칙을 적용 할 수 있는 전하분포인지 파악하고, (물론 가능하니까 문제를 냈겠지만..)
2. 적절한 가우시안 표면 (Gaussian surface) 를 설정하고,
3. 문제에 적절한 수치들을 확인해서 제 자리에 대입하는 것.
두번째, “적절한 가우시안 표면을 설정” 하는게 가장 중요하고, 예제를 통해 확인 할 것도 어떤 상황에서 어떤 형태의 가우시안 표면을 설정했는지 확인하는 것 이다.
적절한 가우시안 표면이 가져야 할 조건은 아래 네 가지 중 하나 이상이다.
1. 가우시안 표면에서 전기장의 크기가 일정하다.
2. 전기장벡터 (E) 와 면적벡터 (dA) 가 평행해서, 두 벡터의 내적이 삼각함수 없는 간단한 형태로 표현 가능하다.
3. 전기장벡터와 면적벡터가 수직이어서 두 벡터의 내적이 0 이다.
4. 가우시안 표면에서 전기장이 0 이다.
물론 전하분포가 충분한 대칭성을 갖고 있지 않아서 가우스 법칙을 적용하지 못하는 경우도 있을텐데, 모든 상황에 적용하지 못한다고 해서 “에이, 가우스 법칙이 틀렸네.” 가 아니라
가우스 법칙을 적용하지 못하기 때문에 계산이 복잡하고 어려워 질 뿐이다.
교재에서는 이걸 이렇게 쓰고 있다.
Gauss’s Law is still TRUE.
예제 24.3
균일하게 양으로 대전된 구의 외부와 내부에 형성되는 전기장을 구해라.

풀이
아래 그림과 같이 대전된 구와 같은 중심을 갖고, 구 보다 큰 반지름을 갖는, 구 형태의 표면을 그려보자.

이렇게 설정한 면이 가우시안 면 이 되는데, 이 면은 앞의 두번째 조건 “전기장 벡터와 면적벡터가 평행하다.” 를 만족한다.
그러면 가우스 법칙의 면적분에 들어있는 벡터 곱을 간단히 쓸 수 있다.
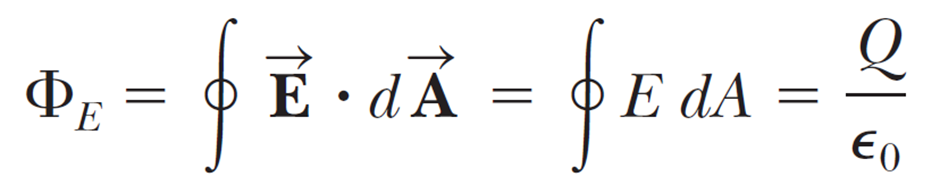
가우시안 면 에서 전기장의 크기는 일정할 테니, 이제 E 는 적분기호 밖으로 꺼낼 수 있고,
남는 표면 적분은 우리가 설정한 구 형태 가우시안 면의 표면적과 같으니까,

이제 전기장만 남기고 이항하면,

구의 중심에 같은 전하량을 갖는 점전하가 놓여있는 경우와 동일한 상황으로 해석이 가능하다는 사실을 알 수 있다.
구의 내부에 가우시안 면을 설정하면 구 내부에 형성되는 전기장을 구할 수 있는데,
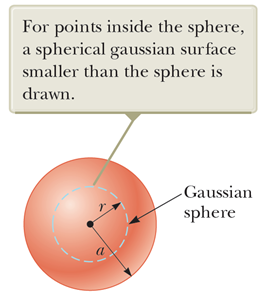
가우시안 면이 작아졌으니까, 그 안에있는 전하량은 더 이상 전체 전하량 Q 가 아니고 다음의 값을 갖는다.

내부의 가우시안 면도 앞의 조건 1, 2 를 만족하므로, 가우스 법칙은 아래의 형태가 되고

여기에 가우시안 면 내부의 전햐량 (qin) 을 대입하고 정리하면,


이제 구 내부와 외부의 전기장이 어떻게 변하는지 한번에 나타내보면,

예제 24.4
균일하게 대전된 무한히 긴 도선에 의한 전기장.

풀이
아래 그림과 같이 실린더 형태의 가우시안 면을 설정하자.

원형의 위 아래 면은 전기장 벡터와 면적벡터가 수직이어서 투과하는 flux 가 0 이므로, 우리가 고려해야 하는 면은 옆면 뿐 이다.
그리고 이 옆면은 앞의 조건 1, 2 둘 을 만족하므로, 가우스 법칙은 다음의 형태가 된다.

A 는 원기둥의 옆면에 해당하는 넓이니까,

정리하면,

예제 24.5>
균일하게 대전된 무한 평행판에 의한 전기장

풀이
아래 그림과 같이 평행판을 관통하는 가우시안 면을 설정하자.

무한도선과 달리 여기서는 원기둥의 옆면이 전기장 벡터와 수직이라 flux 가 0 이고, 원형인 위 아래 면만 가우스 법칙의 계산에 포함된다.
이 원형인 면은 넓이가 A 이고, 두 개 있고,
가우시안 면 안에 있는 전하량을 면전하밀도를 사용해 쓰면,
가우스 법칙은 다음의 형태가 된다.

정리하면,

평행판 문제의 경우 가우시안 면이 반드시 평행판을 관통하도록 설정해야 하는데, 만약 판의 한쪽 공간만 감싸는 면을 설정 할 경우, 아래 그림과 같이 모든 면에서 flux 가 0 이 되기 때문이다.
.

예제 24.6
전기 쌍극자 (electric dipole) 부근, 대전된 원판 (charged disk), 세 꼭지점에 점전하가 놓인 삼각형 같은 경우는 앞의 조건을 만족하는 가우시안 면을 설정 할 수 없기 때문에 가우스 법칙을 적용 할 수 없다.
예를 들어, 대전된 원판의 경우 구 형태의 가우시안 면을 잡으면,

위 그림과 같이 크기가 제각각인 전기장을 얻게 되고,
어떻게해도 앞의 조건을 하나라도 만족하는 가우시안 면을 설정하는게 불가능하다.
가우스 법칙의 응용은 여기까지.
[참고문헌]
주 교재 : Physics for Scientists and Engineers, 9th Edition, Serway/Jewett
'일반물리' 카테고리의 다른 글
| [076-25-01] 전자기학 : 전위와 전위차 - Electric Potential and Potential Difference (0) | 2023.02.08 |
|---|---|
| [075-24-04] 전자기학 : 정전기 평형 상태의 도체 - Conductors in Electrostatic Equilibrium (0) | 2023.02.03 |
| [073] 전자기학 : 가우스 법칙을 이해해보자. (0) | 2022.10.25 |
| [072-24-02] 전자기학 : 가우스 법칙 - Gauss's Law (0) | 2022.10.24 |
| [071-24-01] 전자기학 : 전기 선속 - Electric Flux (2) | 2022.08.18 |