* 이번글은 직접 작성한거라 따로 찾아봐야하는 교재가 없음.
과학 관련 교재들 대부분은 본격적인 내용을 시작하기 전에 그 책을 보는데 필요한 상수들을 모아놓은 페이지를 따로 마련해두고 있다,
물론 우리가 보고 있는 일반물리 교재도 제일 앞에 아래와 같은 상수 모음 페이지가 있다.

이번에는 바로 저 숫자들에 대한 얘기를 살짝 해보자.
우린 질량을 갖는 물체 사이에는 힘이 작용하고, 그걸 만유인력이라 부르기로 했고, 그 힘의 크기는 다음의 계산을 통해 얻을 수 있다는 사실까지 다뤘다.

근데 뉴턴은 만유인력을 아래와 같이 기술했다고 얘기했었는데,

우주의 모든 입자는 입자의 질량의 곱에 비례하고, 둘 사이 거리의 제곱에 반비례하는 힘으로 서로를 끌어 당긴다.
잘 보면, 만유인력에 대한 뉴턴의 정의 어디에도 위 식의 G 를 설명하는 부분은 없다.
그럼 저건 대체 어디서 나온거야.
게다가 상수표를 보면 저 숫자는 말도 안되게 작은 숫자라는걸 알 수 있다.
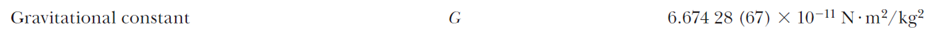
10의 -11 거듭제곱이라니.
보통 머리카락 두께 정도를 얘기할 때 사용하는 마이크로가 10^-6 임을 생각해보면, 대체 저게 얼마나 작은 숫자인지 대충 감이 올 텐데, 그냥 엄청 작다는 정도로 끝나는게 아니라 6.67428 이라는 수치까지 확인 했다고, 그리고 저 숫자는 상황에 따라 바뀌지 않는 상수 (constant) 라고 한다. 언제나 저 숫자를 그냥 가져다 쓰면 된다는 말.

위와 같은 상황에서 두 물체는 서로를 힘 F 로 끌어당기고 그 크기는 위의 식으로 구할 수 있고, 그 과정에 상수 G 가 필요하다는 건데..
단위에 대한 얘기를 먼저 해보자.
만유인력의 크기가 질량의 곱에 비례하고 거리의 제곱에 반비례 한다는 사실이 갖는 단위는 다음과 같다.
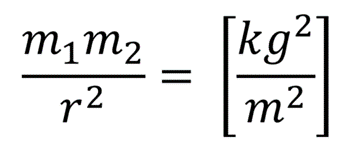
그리고 두 물체 사이에는 힘 이 작용하는데, 우리는 힘을 다음으로 정의 했었다.

그리고 힘의 단위는 뉴턴 [N] 을 쓰기로 했는데, 사실 뉴턴이라는 단위는 질량과 가속도를 곱한 단위를 알파벳 N 으로 줄여 쓰자는 약속 일 뿐이다.

이제 양쪽의 단위를 비교 해보자.

보다시피 질량의 곱에 비례하고 거리의 제곱에 반비례한다는 사실이 갖는 단위는 힘의 단위와 같지 않은데,
이를 해결하기 위해 우리는 아래의 과정을 거쳐 단위 사이에 등호가 성립하도록 해줄 수 있다.

짠.
질량의 곱과 거리의 제곱을 상쇄하고, 힘의 단위만 남겨 줄 수 있는 무언가를 곱하면 우린 두 물체 사이에 작용하는 인력의 크기를 구할 수 있게 된다.
그리고. 곱해진 빨간 부분의 단위는 앞에서 본 만유인력 상수 G 가 갖는 단위와 같음을 알 수 있다.

이제 숫자에 대한 이야기를 해보자.
만약, 질량 10 kg 인 볼링공 두 개가 1m 간격을 두고 떨어져 있을 때,
두 볼링공의 질량의 곱을 거리의 제곱으로 나누면, 100. 일단 단위는 잊자.
약간 억지 스러운 얘기를 잠시 하자면, 10 kg 은 생각보다 무거운 무게인데, 두 볼링공 사이에 작용하는 힘의 크기가 100 에 상응하는 정도라면, 사실 두 공이 실제로 움직여야 하지 않을까? 각 볼링공 질량의 10배에 해당하는 크기의 힘으로 서로를 끌어 당기고 있으니까.
근데 그런일은 일어나지 않지.
여기서 저 숫자 100 에 만유인력 상수를 곱해서 두 볼링공 사이에 작용하는 힘의 크기를 구하면,
6.67428 x 10^-9 N = 6.67428 nN (나노뉴턴) 이라는, 실제로 두 볼링공 사이에는 상상도 하기 어려울만큼 작은 힘이 작용한다는 사실을 확인 할 수 있다.
이러니 안움직일수밖에.
마지막으로,
그럼 대체 저 말도 안되게 작은 숫자는 어떻게 알게된걸까?
그건, 무식하고 미련한 과학자들의 끊임없는 실패에도 굴하지 않는 실험정신이 만들어 낸 기적같은 일 이라고 밖에는 할 말이 없다.
만유인력에 대한 아래 글 에서
1798년에 캐번디시 라는 사람이 어떤 이유로 아래와 같은 실험장치를 고안했고,

이 실험장치가 1800년대에 만유인력상수 G 를 결정 할 수 있도록 하는 중요한 사건 이었음을 살짝 얘기 했었는데,
실제로 만유인력 상수를 비롯한 대부분의 상수들은 끊임없는 실험으로 얻어진 것 들이 많다.
만유인력과 동일한 형태를 갖는 식이 전자기학의 쿨롱법칙에도 나오는데,

두 점전하 사이에는 두 전하의 전하량의 곱에 비례하고, 전하 사이 거리의 제곱에 반비례하는 힘이 작용한다는게 쿨롱법칙이다.
보다시피 형태는 만유인력과 같고, G 가 있던 자리에 새로운 상수가 하나 들어오는데,
저 상수는 아마 분모에는 전하량의 제곱을, 분자는 뉴턴과 거리 (m) 의 제곱을 단위로 가질거라는 생각을 하면서 상수표를 보면,

짠.
단위의 앞에는 역시 오랜 세월 많은 과학자들의 노력으로 얻어진 숫자가 있다.
중고등학생 뿐만 아니라 과학을 공부하거나, 좋아하거나, 어떤 이유로든 숫자를 다루는 일을 하는 사람이라면, 그 숫자가 어떤 단위를 갖는 숫자인지를 항상 눈여겨보는 습관을 들이고, 단위가 갖는 의미를 잠시라도 생각해보면 좋겠다.
[참고문헌]
주 교재 : Physics for Scientists and Engineers, 9th Edition, Serway/Jewett