[021]
공간의 어딘가에 존재하는 입자의 파동함수와 입자를 발견 할 가능성이 높은 평균 위치인 기댓값을 알아봤다. 이제 입자가 특정 구간에 존재하는 경우에 대해 알아볼텐데, 일반적으로 경계조건 아래의 입자 (Quantum Particle Under Boundary Conditions) 또는 상자 속 입자 (Particle in a box) 라 부르는 상황이다.
상자라는 단어를 사용하지만, 입자의 운동은 1차원으로 제한하여 문제를 단순화해서 접근할거고, 양자역학이 조건이나 상황을 분석하고 문제를 해결하는 과정이 고전역학의 방식과 어떻게 다른지 비교적 쉽게 알 수 있는 문제이다.
[021-01] 고전적 입장

우리가 알아보고자 하는 상황을 고전적 입자 개념으로 그려본 그림이다. 하나의 입자가 투과가 불가능한 두 벽 사이를 탄성충돌 하면서 왕복운동 한다면, 일정한 속력을 갖는 입자로 접근해서 상황을 설명하는게 가능하다. 그러면 입자의 운동량 mu 와 입자의 운동에너지는 변하지 않는 값을 갖게 되고, 이를 바탕으로 계를 분석하는게 가능해진다.
이러한 고전적 접근 방식에서 입자의 운동량과 에너지에는 제약이 없다. 연속적인 어떤 값을 가질 수 있고, 만약 입자의 속력이 0 인 즉, 운동량이 0 인 상황도 가능하다.
여기까지가 우리가 다루고자 하는 상황을 고전적인 입자 개념으로 접근한 분석이다.
[021-02] 양자역학적 입장
이 문제를 양자역학의 개념으로 접근하면 상황이 좀 달라진다. 고전 이론에서 입자의 운동량이 문제를 분석하는 실마리 였듯, 이 문제의 조건에 부합하는 적절한 파동함수를 찾는것이 양자역학적 접근의 시작이 된다.

양자역학적 시각으로 볼 때, 벽을 포함한 상황은 위의 그림으로 대체된다. 파동함수를 구하기 위해 벽 사이 공간에 x 좌표를 주었고, 왼쪽 벽을 원점으로 정했다. 투과 불가능한 벽은 무한의 포텐셜 장벽 (potential barrier) 으로 설정하면 파동이 진행하지 못하는 상황을 연출 할 수 있다.
단어들이 좀 생소하지만, 입자가 존재 할 수 있는 구역을 제한하기 위해 일정 거리만큼 떨어진 두 위치에 말 그대로 무한대의 벽을 쌓았다고 생각하면 좀 편하지 않을까 싶다.
[021-03] 경계조건 - Boundary conditions
1. 투과 불가능한 벽이 세워져 있으므로, 양쪽 벽 밖의 영역에서 입자를 발견할 확률은 0 이다. 따라서, 우리가 얻고자 하는 파동함수는 x<0 , x>L 영역에서 0 의 값을 갖는다.
2. 수학적으로 행실이 좋은 (well-behaved) 함수이려면, 모든 공간에서 파동함수는 연속이어야 한다. 따라서, 벽의 외부에서 파동함수가 0 이라면, 벽에서의 파동함수도 0 이어야 한다.
이 조건을 경계조건 (boundary conditions) 이라 하고, 이를 만족하는 파동함수만 고려의 대상이 될 수 있다.
[021-03-01] well-behaved function
우리가 원하는 수학적 스킬을 모두 사용 할 수 있는 함수를 말한다. 쉽게 미분과 적분이 가능한 함수 라고만 생각해도 충분하다. 그리고 미분과 적분이 가능하려면 모든 구간에서 연속인 함수여야 한다.
[021-04] 파동함수 구하기
파동함수를 쓰기 에서 다룬 것 처럼, 이제 위 경계조건에 놓인 입자의 파동함수를 실제 사인파를 이용해서 다음의 형태로 쓸 수 있고, 파장은 입자를 표현하는 드 브로이 파장이다. (아래 식은 슈뢰딩거 방정식에서 유도하기로 하자.)

이 함수가 경계조건 2 를 만족하는지 알아보자. sin 함수는 x=0 지점에서 0 이므로 일단 하나는 만족하고, x=L 에서도 0 이 되어야 한다. 다음의 조건을 만족해야 한다는 말.

sin 함수가 위 조건을 만족하려면,

입자가 가질 수 있는 (허용된) 파장이 n 에 따라 특정 값으로 결정되고, 여기서 n 을 양자수 (quantum number) 라고 한다.
이제 양자수 n에 따라 파장이 결정되는 입자의 파동함수를 다음으로 쓸 수 있다.
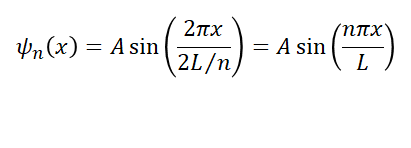
위 함수를 Normalize 하면, A를 구할 수 있고, 완성된 파동 함수는 다음의 형태가 된다.

[021-05] 무슨 말인지 그림을 좀 보자.

양자수 n=1,2,3 인 경우의 파동함수를 그리면 위와 같다.
이전 내용과 연결을 시켜보면, 파동-입자 이중성 때문에 양자 입자라는 개념을 도입했고, 양자입자는 파동의 중첩 즉, 삼각함수의 중첩으로 표현이 가능했다. 이 사실을 특정 영역에 갇혀있는 양자입자에 적용해보니까 입자가 가질 수 있는 파장이 연속적이지 않고 양자화 (Quantize) 되더라는 말이다.
[021-06] 파장과 양자수와 에너지
가열차게 에너지에 대한 이야기까지 달려보자.
양자수에 따라 입자를 표현하는 파동함수의 파장이 제한되기 때문에, 입자의 운동량도 제한을 받게 되는데, 그 값은 드 브로이의 관계에 따라 다음과 같다.
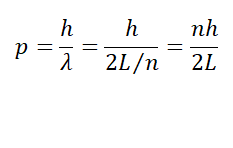
박스 안의 포텐셜 에너지가 0 이니까, 계의 총 에너지는 온전히 입자의 운동에너지 이고, 이 값도 운동량과 같이 양자수에 의해 제한된다. 에너지를 계산해보면,


양자수에 따라 파동함수의 파장이 제한되고, 이에 의해 입자의 운동량과 에너지가 양자화 됨을 이렇게 확인 할 수 있다.
n=1 에 대응하는 상태를 바닥상태 (ground state) 라 하고, 이는 상자속 입자에게 허용된 가장 낮은 에너지 상태를 의미한다. 그리고, 바닥상태가 아닌 입자가 가질 수 있는 에너지는 바닥상태의 에너지의 4베, 9배, 16배 이며, 이 상태를 여기상태 (excited states) 라고 한다.
또, 양자수 n=0 이면 파동함수와 파동함수의 제곱은 0 이 되므로, 물리적으로 아무런 의미를 갖지 못하며, 상자속 입자가 가질 수 있는 가장 낮은 에너지가 0 이 아니므로, 양자역학에 의하면 입자는 정지상태에 있을 수 없다.
이러한 결과는 속력이 0 인 경우를 포함하여, 운동량과 에너지가 연속적인 값을 가질 수 있었던 고전 이론의 해석과 아주 큰 차이가 있다.
[021-07] 파동함수와 확률밀도
파동함수의 절댓값의 제곱 (앞으로는 파동함수의 제곱으로만 쓰자) 을 확률밀도라고 했고, 확률밀도는 입자를 발견할 확률과 관련이 있다고 했었다.
위 파동함수와 그 확률밀도를 비교해보자. 왼쪽은 파동함수, 오른쪽은 확률밀도이다.

양자수가 커짐에 따라 확률밀도가 0 이 되는 지점이 양쪽 벽 말고도 발생하며, 그 갯수가 하나씩 늘어나는걸 확인 할 수 있다.
아니 그럼, 확률밀도가 0 이 되는 지점에서 특정 상태의 입자는 발견 할 수 없다는 말인가?
이게뭐야 대체! 라고 생각이 들겠지만, 이 파동함수의 기댓값을 구해보고, 저 확률밀도와 기댓값의 해석이 어떻게 되는지 알아보자.
[021-07-01] 지금까지 알아 본 상자속 입자의 파동함수를 이용해 이전글에서 다룬 기댓값을 구해보자.
상자속 입자의 파동함수는 다음과 같고,

기댓값은 다음으로 구한다.
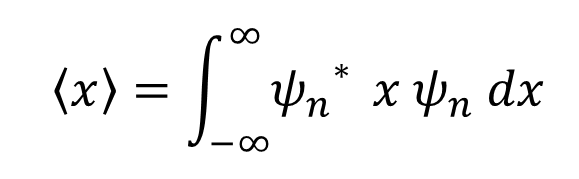
이 둘을 이용해 x 의 기댓값 (평균위치 : average position) 을 구해보면,

sin 을 cos 으로 바꾸고, 부분적분을 하는 아주 귀찮은 과정이 좀 있지만, x 의 기댓값은 양자수 n 에 관계없이 입자가 갇힌 상자의 가운데로 결정된다.
아니 뭐야... 양자수에 따라서 확률밀도가 0이 되는 위치도 달라지고 갯수도 달라진다며... 근데 왜 양자상태에 관계없이 기댓값은 가운데야??
이게 무슨말이냐면, 기댓값을 average position 으로 쓰는걸 보면 알 수 있는데, 말 그대로 입자의 평균위치가 가운데 라는 것이다.
예를 들어, 평균이 50인 둘 혹은 세개의 숫자 모임을 생각해보자. 시험 점수도 상관없다. 40과 60의 평균은 50이고, 20과 80의 평균도 50이다. 또 25, 40, 85의 평균도 50이다. 즉, 평균이 50 이라는 말은 각각의 숫자가 정확히 50인 것과는 별개인 것이다.
이처럼 파동함수가 갖는 특정한 기댓값과 확률밀도는 직접적인 관련이 없다.
[021-08] 정리
구속조건이 주어진 경우, 계를 기술하는 파동함수의 파장은 양자수에 의해 결정되고, 그에따라 계의 운동량과 에너지도 결정되며, 이들 모두는 양자화 되어있다.
동일한 상황의 고전적 입자 개념 접근과 양자역학적 접근은 해석의 차이가 발생한다.
파동함수의 위치의 기댓값과 확률밀도는 직접적인 관련이 없다.
[참고문헌]
주 교재 : Physics for Scientists and Engineers, 9th Edition, Serway/Jewett
'일반물리' 카테고리의 다른 글
| [023] 유한 포텐셜 우물 - A Particle in a Well of Finite Height (0) | 2020.04.08 |
|---|---|
| [022] 슈뢰딩거 방정식 - The Schrodinger Equation (2) | 2020.03.31 |
| [020-02] 파동함수를 쓰기 II (4) | 2020.03.25 |
| [020-01] 파동함수를 쓰기 I (0) | 2020.03.25 |
| [019] 1차원 파동함수와 기댓값 - Expectation Value (0) | 2020.03.23 |