[019]
파동함수가 공간의 특정 위치에서 입자를 발견 할 확률과 관련된다는 이야기까지 했는데, 이번에는 확률에 대해 좀 더 구체적인 이야기를 해보려고 한다.
양자입자라는 개념을 도입하면서, 정확한 운동량을 알고있는 입자는 드 브로이가 제시한 관계에 의해 특정 파장을 갖는 파동으로 표현 할 수 있는걸 알았고, 이 입자는 모든 공간에서 발견될 확률이 동일한 무한히 긴 사인파의 형태가 된다는 것도 알게됐다.
상황을 좀 간단히 보기 위해 입자가 x축 방향의 운동량만 갖는 1차원의 상황을 생각해보기로 하자.
[019-01] x축 위 입자
입자가 x축 방향 운동량만 갖는다고 가정하면, 입자의 파동 함수는 다음의 지수함수 형태가 된다.
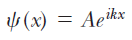
저런 함수는 사실 누구와도 친하지 않으니까, 앞에서 얘기한대로 파동함수는 복소수의 형태를 갖고, 주기나 진폭과 같은 파동의 성질도 함께 가진다는데, 그걸 짧게 쓰면 저런 모양이 되나보다. 정도로 받아들이는게 좀 편하지 않을까 싶다.
실제로 저 식을 풀어쓰면 사인과 코사인으로 구성된 그리고 i 가 붙은 허수부를 갖는 식이 된다. 복소수와 파동을 왜 저렇게 쓰는지도 요청이 있으면 한번 정리를 하기로 하고..
그러면, 임의의 위치 x 의 근방 아주 좁은 구간에서 입자를 발견 할 확률은 위 지수함수의 절댓값의 제곱으로 쓸 수 있게된다.

[019-02] 관심있는 구간에서 입자를 발견 할 확률
이제 적분을 이용하면, x 근방의 아주 좁은 구간 (dx) 에서 입자를 발견 할 확률을 우리가 관심있는 구간에 대한 표현으로 바꿀 수 있다.

위 식은 a 부터 b 까지의 구간에서 입자를 발견 할 확률이 입자를 표현하는 파동함수의 절댓값의 제곱을 적분하여 얻을 수 있다는 말이다.
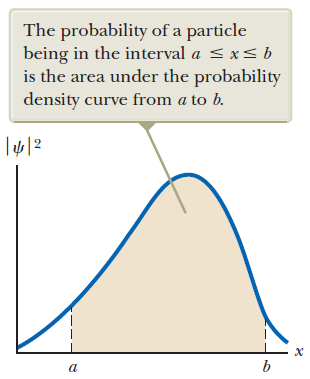
또 다른말로, 우리가 관심있는 구간에서 입자를 발견 할 확률은 파동함수의 절댓값의 제곱으로 둘러싸인 부분의 넓이와 같다고도 할 수 있다.
[019-03] 파동함수의 규격화 - Normalize
이제 앞의 이야기를 "동전을 던져서 앞면이 나올 확률은 50% 이다." 와 같은 표현으로, 좀 현실감있는 말로 바꿔보자.
x축 위 입자를 특정 위치에서 발견 할 확률은 동전에서와 같이 제한적인 값을 갖는데, 바로 0과 1사이의 값이다. 없거나, 있거나, 30% (0.3) 의 확률로 발견 가능하거나.
우리의 지금 논의에서 입자는 x축 어딘가에 반드시 있어야 하니까 우리의 관심을 x축 위 모든 공간으로 확장하면, 즉 x축의 모든 위치에서 입자를 발견할 확률을 모두 더하면 1이 되어야 한다. 이걸 식으로 쓰면,

파동함수의 절댓값의 제곱을 x축의 모든 공간에 대해 적분하면 그 값이 1이 되어야 한다. 이걸 파동함수의 규격화 (normalization) 라 하고, 위 조건을 만족하도록 작업되어 있는 파동함수를 규격화된 파동함수 (normalized wave function) 라고 한다.
마치, 동전 하나를 던져서 앞면이든 뒷면이든 나올 확률이 앞면이 나올 확률 0.5와 뒷면이 나올 확률 0.5를 더해 1이 되는것과 같다.
파동함수의 규격화는 입자가 공간의 어딘가에는 반드시 존재한다는 아주 단순한 사실을 표현 한 것이다.
[019-04] 기댓값 - Expectation value for position x
입자가 어딘가에는 반드시 있다는 믿음을 가지고, 그럼 어느 위치에서 입자가 발견될 가능성이 가장 큰 가 에 대한 이야기도 할 수 있을텐데, 이 평균적인 위치 (average postion) 를 위치 x의 기댓값 (expection value) 라고 한다.
기댓값은, 입자를 찾아내고 싶은데, 도무지 어디쯤 있을지 알지못하면 막무가내로 위치를 바꿔가면서 끊임없이 측정을 해야 하는데, 수학적으로 찾아낼 수 있는 큰 기대를 할만한 위치를 알아 낼 수 있다는 의미이기도 하다.
기댓값은 다음으로 정의한다.
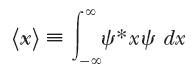
파동함수와 파동함수의 켤레 복소수 사이에 x 를 넣고 (곱하고), 이를 x의 모든 공간에 대해 적분하면, 입자를 발견 할 가능성이 가장 큰 위치가 톡 튀어나온다.
예를 들어, 쌀 가마니가 거실에서 터졌다면, 일단 짜증부터 나겠지만, 쌀 알갱이를 발견 할 확률이 가장 높은 곳은 거실일테니, 위 식의 기댓값은 거실이 된다. 물론, 거실하고 주방이 연결되어 있다면 쌀 알갱이의 일부는 주방 바닥에서 발견되겠지만, 짜증이 많이 난 우리는 아마 거기에 큰 기대를 하지는 않을거다. 또 하루 이틀정도 후에 왠지 쌀 알갱이가 안방 바닥에서도 나올지 모르지만, 이정도 가능성은 배제하는게 정신건강에 이로울거다.
이렇게 다양한 상황들이 존재 할 수 있으니까, 기댓값에 대한 식을 좀 더 일반화 해서 쓰면 다음으로 쓸 수 있다.
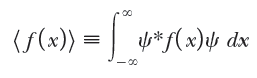
많이 억지스러운 예를 들었는데, 어떤 계를 기술하는 파동함수를 정확히 알면, 우리가 원하는 어떤 값을 알아내는게 가능하다는 의미이다.
[019-05] 정리
이야기를 좀 간단히 하기 위해 x축 위에 존재하는 하나의 입자를 도입했고, 그 입자를 발견할 확률이 실제로 어떻게 계산되는지 알아봤다.
특정 구간에서 입자를 발견 할 확률은 파동함수의 절댓값의 제곱을 적분하여 얻을 수 있고. 입자가 공간의 어딘가에는 반드시 존재한다는 사실에서 파동함수의 규격화를 이야기 했다.
파동함수와 켤레 복소수를 이용하여 적절한 계산을 하면, 우리가 입자를 발견 할 가장 큰 기대를 할 수 있는 위치를 알 수 있으며, 이를 위치에 대한 기댓값 이라고 한다.
[참고문헌]
주 교재 : Physics for Scientists and Engineers, 9th Edition, Serway/Jewett
'일반물리' 카테고리의 다른 글
| [020-02] 파동함수를 쓰기 II (4) | 2020.03.25 |
|---|---|
| [020-01] 파동함수를 쓰기 I (0) | 2020.03.25 |
| [018] 파동함수 - The Wave Function (0) | 2020.03.21 |
| [017] 양자역학 시작하기 전에 (0) | 2020.03.17 |
| [016] 불확정성 원리 - The Uncertainty Principle (0) | 2020.03.16 |