[016]
이제 교재에서 다루는 양자물리학의 소개에 관한 내용은 이중슬릿 실험을 한번 더 살펴보는 것과 불확정성 원리에 대한 내용 두 가지가 남았는데, 이중슬릿 실험은 여기에서 실험 장치와 결과만 간단히 정리하려고 한다.
불확정성 원리는 양자화, 파동-입자 이중성과 함께 양자 물리학의 근간을 이루는 세 가지 개념 중 하나로, 흑체복사, 광전효과, 콤프턴효과, 드 브로이 물질파에 대한 이야기를 통해 양자화와 파동-입자 이중성에 대한 내용을 다뤘고, 마지막으로 불확정성 원리에 대한 이야기를 해보자.
[016-01] 이중슬릿 실험
책이든 인터넷이든 양자물리학에 관한걸 찾으면 빠지지 않고 나오는게 이중슬릿 간섭 실험이다. 여기서 실험장치의 구성과 결과를 간략히 정리하고 넘어가자.
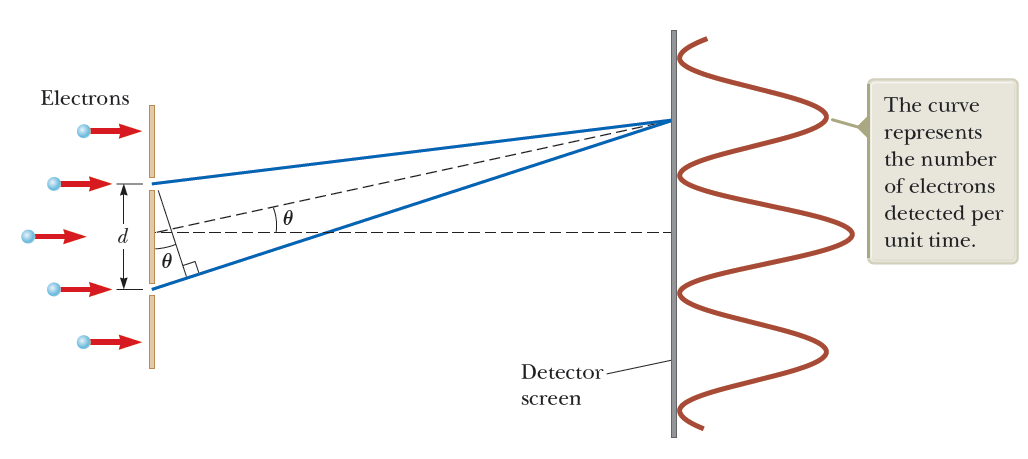
거리가 어느정도 떨어져 있는 두 개의 구멍이 난 벽이 있고, 구멍 난 벽으로부터 또 어느정도 거리가 떨어진 곳에 전자를 검출 할 수 있는 스크린을 설치하자.
스크린의 반대편에서 두 개의 구멍이 있는 벽을 향해 많은 전자를 쏘면, 파동에서 일어나는 간섭무늬가 발생한다. 라는게 이중슬릿 실험의 결과이다. 전자를 입자로 생각한다면, 구멍과 대응되는 위치에 전자들이 도착해서 아마 두 개의 무늬가 생길텐데, 마치 전자가 두 개의 구멍을 동시에 통과한 것 처럼 간섭 무늬가 나타나며, 파동의 간섭을 설명하는 식으로 보강/상쇄 간섭의 발생 위치를 기술 할 수 있더라는거다.
이 역시 입자로 알고있는 전자의 파동적 성질에 대한 실험인데, 앞서 논의한 양자모델을 도입하면, 전자는 공간 전체에 존재하는 파동의 조합으로 만들어진 것 으로 생각 할 수 있고, 전자를 구성하고 있는 이 파동의 성분들은 동시에 두 구멍을 통과 할 수 있다는 접근이 가능하다. 여전히 불편하긴 마찬가지지만..
[016-02] 불확정성 원리 - The Uncertainty Principle

고전물리에서 우리는 어떤 물체의 초기 상태 - 위치와 속도 - 를 알면, 얼마의 시간이 흐른 후, 물체의 위치와 속도를 알 수 있다고 배웠는데, 여기서 말하는 물체의 위치와 속도를 동시에 정확히 측정 할 수 없다는 것이 불확정성 원리이다.
1927년 Werner Heisenberg 는 이 내용을 다음으로 제시한다. 여기서 플랑크상수에 취소선 같은게 하나 더 그어진건 플랑크상수를 2파이 로 나눈 값이다.


위치의 불확실성과 운동량의 불확실성은 동시에 줄일 수 없고, 그 둘의 곱은 어떤 숫자보다 항상 크다. 로 해석 할 수 있는데, 입자의 위치를 정확히 알아낼수록 입자의 다음 위치의 불확정성은 커지고, 입자의 운동량 (속도) 을 정확히 알아낼수록 입자의 위치의 불확정성이 커진다. 는 말이다.
하여튼, 어떤 입자의 위치와 운동량을 동시에 알아내는데에 한계가 있다는 말이다.
[016-03] 드 브로이 물질파와 연결해서 생각해보자.
정말, 가면 갈수록 어려운듯 하지만, 이렇게 한번 생각을 해보자.
우리가 파장을 정확히 알고있는 입자를 상상해보자. 드 브로이에 따르면 입자는 이 하나의 파장에 대응하는 운동량을 가질텐데, 이 파장이 공간에 어떻게 존재하느냐면,

위의 그림처럼 파장이 일정하니까, 공간상에 위치를 특정 할 수가 없다. 즉, 정확한 운동량을 안다는건 위치에 대한 무한대의 불확정성을 갖게 된다는, 위치에 대해서 정말 아무것도 모르는 상태가 된다는 말이다. 입자의 운동량에 대한 완전한 정보는 입자의 위치에 대한 모든 정보를 잃는 댓가인 것이다.
상황을 좀 바꿔서, 입자가 가질 수 있는 운동량의 "범위" 를 알고 있다고 생각해보자. 이전과 마찬가지로 드 브로이의 접근에 따라 우리는 입자가 가질 수 있는 파장의 "범위" 를 알게 되고, 정확한 운동량을 알고있었던 경우와 달리 입자는 하나의 파장으로 기술되지 않으며, 해당 범위의 파장을 갖는 파동의 조합으로 표현된다. 즉, 웨이브패킷이 만들어지는 것.
만약에 입자가 어디있느냐고 누가 물어보면, 웨이브패킷이 정의되는 영역 어딘가에 있다. 정도로는 얘기 할 수 있게 된다. 양자 입자에 대한 이전 글에서 논의 한 대로 단일 파장을 갖는 파동과 달리 웨이브패킷이 형성되는 공간은 위치를 특정할 수 있었으니까.
정확히 알고있던 입자의 운동량을 약간 멍청하게 알게되니까, 전혀 몰랐던 입자의 위치에 대한 정보도 약간 멍청하게 알게 된거다! 멍청하다는 표현을 사용했지만, 대단한 결과인거지.
또 만약, 운동량에 대한 정보를 모두 잃는다면, 모든 가능한 파장을 갖는 파동의 중첩이 가능해지므로 길이를 갖지 않는 (zero length) 의 웨이브패킷을 만들어 낼 수 있게되므로, 정확한 위치를 특정 할 수 있게 될거다.
[016-03-01] 도무지 이게 무슨말인지 이해가 안되니까 예제 하나만 보자.
Q : 전자의 속력이 5 x 10^3 m/s 로 측정되었고, 정확도가 0.003 % 이다. 이 전자의 위치의 불확정성은 얼마인가?
A : 전자의 속력이 x축 방향이라 가정하면, 운동량은 다음으로 구할 수 있다.
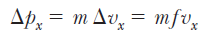
여기서 f 는 속력의 정확도 이다. 불확정성 원리에 따른 위치의 불확정성은,

전자가 0.386 mm 의 길이 "어딘가"에 있을 수 있다는 이야기 인데, 원자의 크기를 생각한다면, 그냥 어디 있는지 여전히 모르는 수준이긴 하다.
[016-04] 주의사항
불확정성 원리를 다루면서 주의 할 점은, 위치와 운동량의 측정이 시스템과 간섭을 일으켜 생기는 결과가 아니라는 것이다.
전자를 관측하기 위해 광학현미경을 사용하는 경우를 생각해보자. "전자가 관측됐다" 는 것은 관측에 필요한 광자와 전자가 충돌했다는거고, 그러면 광자는 전자의 움직임을 야기하니까 운동량의 정확도가 떨어진다는 이야기가 아니다.
우리는 불확정성을 얘기하는 동안 측정이나 관측에 대한 이야기는 전혀 하지 않았다. 물질파와 연결한 이야기와 마찬가지로 불확정성 원리는 측정 프로세스와 무관하게, 물질이 갖는 파동적 특성 때문에 발생하는 매우 근본적인 구속이다.
[016-05] 정리
여기까지의 이야기로 현대물리의 커다란 이론 두 가지 - 상대론과 양자물리학 - 를 정말 기초적으로 알아봤다.
양자화, 파동-입자 이중성, 불확정성 원리를 근간으로 하는 양자물리학의 도입을 다뤘으니까 이제 양자역학을 다룰 차례이긴 한데, 양자역학은 시작이 파동함수여서 수학을 배제하고는 진행 자체가 불가능하고, 고등학교 수준 이상의 삼각함수와 파동이론, 에너지개념 등을 그냥 첫 페이지부터 막 갖다 써야 하기때문에 사실 블로그에 글로 설명하는데에 한계가 많다.
그래도 시도는 해 볼까.. 하는 생각이 있긴 한데.. 일단 수식을 최대한 빼고 정리하는 노력은 해봐야겠다.
웨이브패킷 (wave packet) 은 아래 링크 참조
[015] 새로운 모델 : 양자 입자
[015] 이전글의 말미에 적은대로 이제 파동을 이용해서 과연 입자와 같은 성질을 갖도록 하는게 가능한지 알아 볼 차례다. 빛의 이중성 - 파동과 입자의 특성을 모두 가짐 - 에 관한 이야기를 시작하면서 부터 계..
physicslog.tistory.com
[참고문헌]
주 교재 : Physics for Scientists and Engineers, 9th Edition, Serway/Jewett
'일반물리' 카테고리의 다른 글
| [018] 파동함수 - The Wave Function (0) | 2020.03.21 |
|---|---|
| [017] 양자역학 시작하기 전에 (0) | 2020.03.17 |
| [015] 새로운 모델 : 양자 입자 - Quantum Particle (2) | 2020.03.13 |
| [014] 입자의 파동적 성질 - Wave Particle Duality (0) | 2020.03.12 |
| [013] 전자기파동의 본질 - Electromagnetic Wave (0) | 2020.03.10 |