[015]
이전글의 말미에 적은대로 이제 파동을 이용해서 과연 입자와 같은 성질을 갖도록 하는게 가능한지 알아 볼 차례다.
빛의 이중성 - 파동과 입자의 특성을 모두 가짐 - 에 관한 이야기를 시작하면서 부터 계속 하는 말은 "빛이든 물체든 입자와 파동의 특성을 동시에 갖는다는 사실을 받아들이기가 불편하다." - 난 어렵다기보다는 불편한게 맞다고 생각한다 - 는 것인데, 이에 관한 모든 실험들이 이 사실을 증명하고 있으니 일단 받아들여 보자.
그런데, 넓은 마음으로 "그래, 오케이" 하고 나니 또 문제가 되는건, 우리가 지금까지 알고있는 모델 - 입자모델, 파동모델 - 각각으로는 두 특징 모두를 갖는 개념을 만들 수가 없다는것이다. 전자만 생각해봐도 우리는 원자핵주위의 특정 궤도를 따라 움직이는 음전하를 가진 입자로 알고있는데, 여기에는 어떠한 파동적 설명도 포함되어 있지가 않다.
그래서, 두 가지 특징을 모두 갖는 양자입자 라는 새로운 모델을 도입하려는데, 당연히 이 모델은 입자모델과 파동모델을 조합해서 만들어져야 할거다.
[015-01] 입자와 파동의 특징
입자가 갖는 가장 명확한 특징은 입자가 차지하고 있는 공간의 위치를 특정 할 수 있다는 것 (localize) 이다. 이와 달리 특정 주파수를 갖는 무한히 긴 파동은 존재하는 위치를 특정 할 수가 없다. 깜깜한 밤에 거실에 있는 TV를 켠다고 생각해보자. 아마 일부러 막은 공간이 아닌 이상 빛이 퍼져 나갈텐데, 그 파동의 위치를 특정 할 수 있을까?
이제, 이 무한히 긴 파동이 존재하는 공간을 입자처럼 한정적이 되도록 만들어보자. 즉, 파동에 입자의 고유한 특성을 부여해 보자는 말.
[015-02] 글로 하는 설명 - 뒤에 어쩔 수 없이 식으로 하는 설명도 있음.

위 그림과 같이 일정한 주파수를 가지고 무한히 긴 파동을 하나 생각해보자. 편의를 위해 파장은 x축 위에 존재하고, 마루(crest) 중 하나가 중심 (x=0) 에 위치한다고 가정하자.
이제 두번째 파동을 도입할건데, 이 파동은 첫번째 파동과 같은 진폭을 갖고 주파수만 다르다. 첫번째와 마찬가지로 두번째 파동도 x축 위에 존재하고, 마루 중 하나가 중심에 위치한다고 가정하자.
그리고, 이 두 파동을 중첩 (superposition) 시키면 다음과 같이 새로운 파동이 만들어진다.

중요한점은 두 파동을 중첩시키자 위치에 따른 파동의 특성이 달라졌다는 것 이다. 중첩 전의 두 파동은 모든 공간 - 물론 x축 - 에서 같은 특징이 나타났는데, 중첩된 파동은 두 파동의 보강/상쇄 간섭이 발생하면서 위치 마다의 차이가 생긴것이다.
이제 여기에 새로운 파동을 계속 중첩 시킬건데, 두번째 파동을 도입할때와 마찬가지로 다음 두 가지 주의사항이 있다.
1. 새로운 파동의 마루가 x=0 에 있을 것
2. 더해지는 모든 파동의 주파수가 다를 것
위 조건을 만족하는 파동을 계속 중첩하면, 파동의 마루가 겹쳐진 위치 x=0 를 제외한 모든 위치에서 파동은 계속되는 상쇄간섭 때문에 진폭을 잃는다. 이 결과로 보강간섭만 일어난 작은 구간을 얻게 되는데 이를 wave packet (웨이브패킷 : 파속) 이라고 하며, 그림으로는 아래와 같이 표현된다.

여기까지하면 우리는 웨이브패킷 - 파속 이라는 단어가 어색해서 그냥 이걸로 써야겠다. - 이 공간의 특정한 위치를 점유하게 된다는 것, 즉 입자와 같은 특성을 갖게 된다는 것을 알 수 있다.
웨이브패킷의 위치를 입자의 위치로 말 할 수 있다는 것이다.
여기까지가 말로하는 설명이었고, 웨이브패킷의 다른 입자적 특성은 어쩔 수 없이 수학이 좀 들어가야 한다.
[015-03] 웨이브패킷 1/2 - 수학이 약간 있음
파동의 중첩으로 만들어진 웨이브패킷이 공간의 특정 위치를 점유한다는 것 (localize) 은 우리가 새로 도입하기로 한 양자 입자의 단 하나뿐인 입자적 특성이라서, 웨이브패킷이 질량이나 전하 같은 다른 입자적 특성을 갖는지는 아직 알 수가 없다. 따라서, 정말 파동의 중첩으로 입자가 만들어졌다는 생각이 전혀 들지 않을텐데, 이제 웨이브패킷이 다른 입자적 특성을 갖는다는걸 확인해보자.
이야기의 처음으로 돌아가서 파동이 두 개인 경우부터 생각해보자.
중첩 이전의 두 파동은 진폭이 갖고, 진동수가 달랐다. 그러면 각 파동은 다음으로 쓸 수 있는데,

사인파로 합성해도 같은 결과를 얻지만, 코사인을 선택하면 모든 파동의 마루가 저절로 x=0 에 위치하게 되니까 코사인으로 시작했다.
여기서 파수와 각진동수는 다음과 같다.

... 파동이 삼각함수로 써지고, 코사인 뒤에 붙은 뭔가 복잡해보이는 저 모양이 나오는건 요청이 있으면 정리해서 올리겠다.
이제 저 두 파동을 합치면,

삼각함수의 합을 해야하니까 고등학교 다닐때 언젠가 배웠을 다음 식을 이용하자.

그러면 다음을 얻는다.
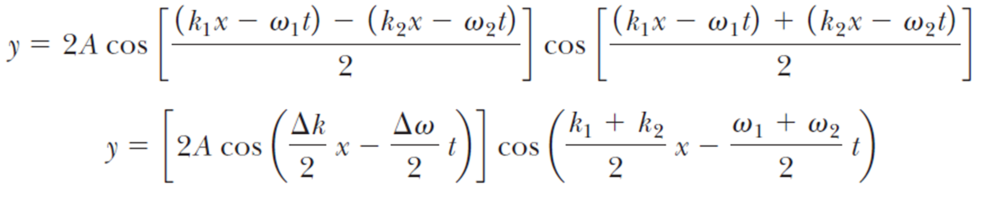

수학때문에 정신없으니까 섹션을 좀 나눠보자.
[015-04] 웨이브 패킷 2/2
중첩의 결과로 얻은 식과 그래프를 먼저 보고 시작해보자.

중첩 파동의 식을 약간 나누어 보면 앞에 곱해진 파란 박스 부분도 하나의 파동의 형태를 갖고 있는데, 이를 파동 봉투 (envelop of the wave) 라고 한다. 중첩에 의해 생긴 반복되는 구간이 일정한 규칙을 가지고 움직이는구나 로 생각하면 좀 편하려나..
이 봉투는 중첩 이전의 두 파동과는 다른 속도를 갖는데, 파동의 위상속도가 파수와 각진동수로 다음과 같이 기술됨을 고려하면,

위상속도는 시간변수 t 의 계수와 공간변수 x 의 계수의 비율로 결정된다.
봉투도 파동과 동일한 형태로 기술되니까, 봉투의 위상속도도 위와 같은 방식으로 결정될텐데, 다음과 같다.

여기서 아랫첨자 g 는 group 의 첫 글자이다. - 군속도 -
위 식은 두 파동의 중첩의 결과니까, 아주 많은 파동이 이 과정을 통해 중첩되면 이 비율은 다음의 형태가 된다.

여기에 플랑크상수를 포함하는 항을 곱하고 나누는 과정을 하면,

봉투의 속도가 에너지를 운동량으로 미분한 값과 같다는 결과를 얻게 된다.
여기까지를 정리하면,
아주 많은 파동을 중첩하면 웨이브패킷을 얻을 수 있는데, 이 웨이브패킷의 속도는 에너지와 운동량을 이용해 기술 된다. 는 것이다.
[015-05] 웨이브 패킷의 입자적 특성
우리는 지금 파동에 입자적 특성을 부여하는 중 이었음을 다시한번 생각하고, 이야기를 진행해보자.
속도 u로 움직이는 자유입자 (free particle) 를 생각해보자. 이 입자의 총 에너지는 운동에너지와 같을텐데,

총 에너지를 운동량으로 미분하면, 어렵지 않게 입자의 속력을 얻게 된다.

그런데 말입니다... 에너지를 운동량으로 미분하면 뭐였다고...?

봉투의 속도가 입자의 속도와 같음을 확인했고, 이야기가 좀 길었지만, 파동을 중첩하여 웨이브패킷을 만드는 것이 입자의 특성을 가질 수 있다는 의미있는 근거를 갖게됐다.
[015-06] 정리
파동과 입자의 특성 모두를 갖는 양자입자라는 개념을 도입하려고, 파동의 중첩을 이용했다.
아주 많은 파동을 중첩하면 순수하게 보강간섭만 일어난 구간을 얻을 수 있는데 이를 웨이브패킷 이라 한다.
웨이브패킷은 파동봉투 (enlvelop of wave) 로 표현 하는 수학적 파동의 형태를 포함하는데, 봉투의 속력은 에너지의 운동량에 대한 미분으로 기술 할 수 있다.
자유입자의 총 에너지를 운동량으로 미분하면 입자의 속력을 얻을 수 있다.
봉투의 속력 = 에너지의 운동량 미분 = 입자의 속력 의 관계에서, 파동의 중첩으로 웨이브패킷을 만드는것이 입자적 특성을 가진다는 유의미한 근거를 가질 수 있게 됐다.
여기까지,
양자 개념의 도입에서 시작하여, 파동의 입자성, 입자의 파동성 (이중성) 을 거쳐 파동이 입자적 특성을 가질 수 있다는 것 까지 다루었고, 양자역학으로 넘어가기 전 불확정성 원리 정도를 다루는게 남았다.
교재 순서에는 불확정성 원리 전에 이중슬릿 실험에 관한 섹션이 하나 나오는데, 내용을 좀 보고 둘로 나눌지 하나로 쓸지 생각해봐야겠다.
그리고, 양자역학은 정말 그냥 수학이 많아서 여기에 정리를 하는게 맞나 고민중이다. 만약 양자역학으로 넘어가지 않으면 교재 앞으로 돌아가서 일반물리 내용을 계속 다룰거다.
[참고문헌]
주 교재 : Physics for Scientists and Engineers, 9th Edition, Serway/Jewett
'일반물리' 카테고리의 다른 글
| [017] 양자역학 시작하기 전에 (0) | 2020.03.17 |
|---|---|
| [016] 불확정성 원리 - The Uncertainty Principle (0) | 2020.03.16 |
| [014] 입자의 파동적 성질 - Wave Particle Duality (0) | 2020.03.12 |
| [013] 전자기파동의 본질 - Electromagnetic Wave (0) | 2020.03.10 |
| [012] 콤프턴 효과 - The Compton Effect (0) | 2020.03.09 |