* 이번 내용은 그림을 먼저 쭉 훑어보고 글을 보는 것을 추천. 그림을 보고 직관적으로 알게 되는것도 항상 중요하다.

우리는 전기장을 위의 수학적 형태로 정의하기로 했는데, 전기장이 그림으로는 어떻게 표현 되는지 알아보자.
전기장 선 (electric field lines) 을 이용해 전기장을 시각화 하는 방법은 패러데이가 처음 시도했는데, 그 과정은 다음의 규칙을 따른다.
말이 좀 어색 할 수 있는데, 그림과 같이 보면서 이해해 보기로 하자.
- 모든 위치에서 전기장 벡터는 전기장 선에 접한다. 전기장 선은 화살표로 표시하는 방향을 갖고, 이 방향은 전기장 벡터의 방향과 같다. 이 방향은 전기장이 형성된 공간에 양전하를 두었을 때, 양전하가 받는 힘의 방향과도 같다.
- 전기장 선에 수직인 표면을 통과하는 단위면적 당 전기력선의 수가 많을수록 전기장의 크기는 크다. 따라서, 강한 전기장이 형성된 공간은 전기장 선을 촘촘하게 그리고, 약한 전기장의 경우에는 전기장 선을 드문드문 그린다.
위 내용을 아래 그림에 적용해보자.

면적 A 를 통과하는 전기장 선의 밀도가 높으니까 A의 전기장이 B 보다 크고, 각각의 위치마다 화살표의 방향이 다르니까 이 전기장은 균일하지 않다 라고 할 수 있다.
두 면적을 통과하는 전기장 선의 개수가 같으면 전기장의 세기가 같은게 아니냐고 생각 할 수 있지만, 단위면적 당 지나는 전기장 선의 수가 전기장과 비례하는 것이지 전체 전기장 선의 개수와 관계 있는게 아니다.
이제 또 하나의 궁금증이 생길 수 있다.
과연 이런 규칙으로 그린 전기장 선의 갯수/밀도 와 쿨롱의 법칙으로부터 얻은 전기장의 수학적 표현이 같은 의미를 갖는다고 믿어도 되나?
눈에 안보이는거라고 그냥 대충 적당히 꾸며낸 얘기 아니야?
물론 그럴리가 없지.
저 질문에 대한 답을 알아보기 위해,
중심에 점전하가 위치하고, 반지름이 r 인 구 형태의 공간을 상상해보자.
아주 당연하게 구의 대칭 때문에 구의 표면 모든 위치에서 전기장의 세기는 같다. 구의 표면은 모두 구 중심의 점전하로부터 같은 거리만큼 떨어져 있으니까.
이제, 구 중심의 점전하로부터 N 개의 전기장 선이 방출(?) 되는 상상을 해 보면, 구의 표면을 관통하는 전기장 선의 개수도 N 개 임을 알 수 있다.
중심에서 N 개가 출발 했으니 r 만큼 떨어진 구 표면 전체를 뚫고 지나는 전기장 선의 갯수도 N 개 여야 한다.
우리는 전기장 선의 총 개수가 아니라 단위면적당 개수가 중요하다고 했으니, 이렇게 방출된 N 개의 전기장 선을 구의 표면적으로 나누면,
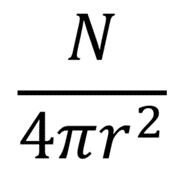
짠.
N 과 π 가 상수니까 그림으로 생각해 본 전기장의 세기는 r 의 제곱에 반비례하는데,
이 사실은 쿨롱법칙에서 얻은 다음의 관계과 정확히 같은 의미를 갖는다.

전기장의 크기는 거리의 제곱에 반비례.
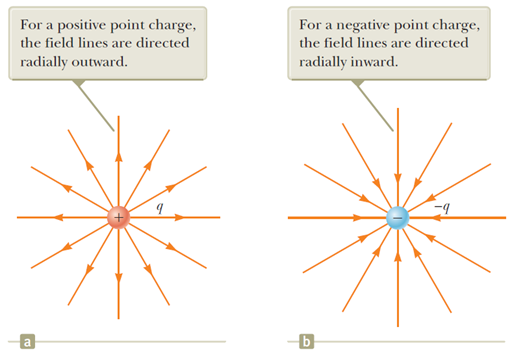
위 그림은 하나의 양/음 점전하에 의해 주변에 형성되는 전기장을 전기장 선으로 나타낸 것 이다.
물론 우리는 3차원 공간에 살고 있으니까, 실제로는 표면이 아니라 공간의 모든 방향으로 화살표가 그려져야 한다고 이해해야 한다.
앞에서의 약속을 따라, 위의 점 전하들이 있는 공간 근처에 양전하를 갖는 입자를 놓으면, 원천전하가 양전하인 경우(a)는 밀려나고, 음전하인 경우(b)는 끌려올 테니 그 방향과 동일한 화살표로 전기장의 방향을 표시했다.
약간 어려운 얘길 추가하자면,
위에 표시된 전기장 선은 점전하로부터 어느정도까지만 그려지는게 아니라 무한한 길이로 그려지는게 올바르고,
또, 원천전하에 가까워 질수록 전기장 선은 촘촘해지니까 전기장의 세기 역시 세진다.
주의사항은, 전기장 선이 입자의 운동경로를 표현하지 않는다는 것.
위의 경우처럼 단 하나의 점전하가 전기장을 형성하고, 그 주변에 단 하나의 점전하가 놓이는, 일부러 설정 한게 아닌 이상 현실에서 일어날 수 없는 아주아주 특별한 상황을 제외하고,
전기장 선은 해당 공간에서 입자의 운동경로와는 아무런 관련이 없다.
이제 둘 이상의 전하가 형성하는 전기장을 전기장 선으로 나타내는 규칙을 알아보자,
- 전기장 선은 양전하에서 출발하고, 음전하에서 끝난다. 전하의 균형이 맞지 않으면, 초과되는 몇 개의 전기장 선은 시작 혹은 끝이 무한히 먼 곳으로 발산한다.
- 양전하에서 시작하거나 음전하에서 끝나는 전기장 선의 개수는 전하량에 비례하도록 그린다.
- 둘 이상의 전기장 선이 교차하지 않도록 한다.
위 설명 역시 그림으로 보면 훨씬 직관적일텐데,
예를 들어, 1C 의 양/음전하에 여섯개의 전기장 선을 그리기로 약속 했다면, 2C 의 전하에서 출발/도착하는 전기장 선은 열두개를 그리자는 말이다. 물론 이 개수는 정해지지 않았고, 그저 효과적으로 표현 할 수 있을정도면 된다.
아래 그림을 보자.

위 규칙대로, 양전하에서는 출발하는 전기장 선을, 음전하에는 도착하는 전기장 선을 그렸고, 각 전하에 연결된 전기장 선의 개수가 같은걸 보니, 전하량은 같고 부호가 다른 두 전하에 의한 전기장을 표현 했음을 알 수 있다.
위와 같은 형태의 전하 분포를 전기 쌍극자 (electric dipole) 이라 하는데, 뒤에 자세히 다룰 상황이 있다면 그 때 알아보기로 하고, 여기서는 저런 단어가 있구나. 정도만 알고 넘어가자.

앞서와 겹치는 얘기는 넘어가고,
위와 같이 가까이 있는 두 양전하에 의한 전기장 선은 저렇게 그려지는데, 음전하가 없으니까 전기장 선이 도착 할 데가 없고, 결국 모든 전기장 선은 무한히 먼 곳으로 발산만 하는 형태가 된다.
또, 위 분포에서 아주 먼 위치에서의 전기장은 2q 의 전하량을 갖는 하나의 점전하에 의한 전기장과 크기가 거의 같아진다.
마지막으로, 동일하지 않은 전하량을 갖고 가까운 거리에 있는 양전하와 음전하의 경우를 알아보자.

양전하의 전하량이 두 배 크니까, 양전하에서 출발하는 전기장 선이 두 배 더 많을테고, 그럼 절반의 전기장 선은 양전하에서 출발했지만 음전하에 도착하지 못하고 무한대로 발산하고 만다.
앞의 양전하 두 개와 유사하게,
두 양/음전하 사이의 거리보다 훨-씬 먼 위치에서 전기장의 크기는 +q 의 양전하 하나에 의한 전기장의 크기와 거의 같아진다.
전기장 선은 실제하는게 아니다. 끌어 당기는 힘만 작용하는 중력장과 다르게 작동하는 전기장을 좀 더 이해하기 쉽게, 수학적인 기술/설명과 어긋남이 없도록 눈으로 알아 볼 수 있게 고안한 표현 방식이다.
이번글은 여기까지.
[참고문헌]
주 교재 : Physics for Scientists and Engineers, 9th Edition, Serway/Jewett
'일반물리' 카테고리의 다른 글
| [071-24-01] 전자기학 : 전기 선속 - Electric Flux (2) | 2022.08.18 |
|---|---|
| [070-23-07] 전자기학 : 균일한 전기장 속 하전입자의 운동 - Motion of a Charged Particle in a Uniform Electric Field (0) | 2022.07.13 |
| [068] 전자기학 : 전하분포에 의한 전기장 문제 (0) | 2022.06.23 |
| [067] 누리호와 중력 그리고 구심력 (0) | 2022.06.22 |
| [066-23-05] 전자기학 : 연속 전하 분포에 의한 전기장 - Electric Field of a Continuous Charge Distribution (0) | 2022.06.21 |