[068] 전자기학 : 전하분포에 의한 전기장 문제

전하가 분포되어 있는 세 가지 형태에 따라서 특정 위치에서의 전기장을 어떻게 구하는지 예제를 통해서 확인해보자.

 

 

사실 문제 풀이는 거의 다루지 않는 편인데, 전자기학은 접근을 어떻게 하느냐에 따라 완전히 틀린 결과를 얻는 경우가 아주아주 많기 때문에 어려운 문제를 만나기 전에 접근 방식부터 알아두고자 따로 작성하게 됐다.

 

 

전하의 연속 분포에 의한 전기장에 대한 아래 글을 먼저 보고 와도 좋다.

https://physicslog.tistory.com/entry/066-23-05-%EC%A0%84%EC%9E%90%EA%B8%B0%ED%95%99-%EC%97%B0%EC%86%8D-%EC%A0%84%ED%95%98-%EB%B6%84%ED%8F%AC%EC%97%90-%EC%9D%98%ED%95%9C-%EC%A0%84%EA%B8%B0%EC%9E%A5-Electric-Field-of-a-Continuous-Charge-Distribution

[066-23-05] 전자기학 : 연속 전하 분포에 의한 전기장 - Electric Field of a Continuous Charge Distribution

 

 

 

[068-001] 대전된 막대기 (선형 분포) 에 의한 전기장

 

 

길이 l 의 막대에 전체 양의 전하량 Q 가 선 전하 밀도 λ 로 대전되어 있고, 이 막대에 의해 위치 P 에 형성되는 전기장의 크기를 구하는 문제다.

편의상 막대는 부피가 없고 길이만 갖는걸로 가정하자.

 

앞의 글에서 전하를 띄고 있는 물체에 의한 전기장은 물체를 아주 작게 나누고, 각 조각에 의한 효과를 모두 더하는 과정을 거쳐 구할 수 있고, 그 결과는 다음의 식으로 쓸 수 있다고 했는데,

 

위 그림에서 아래 적분의 피적분 함수를 딱 떠올리는건 쉽지 않고, 그래서 우리는 저 막대를 아주 작게 나눈다는 상상부터 하기로 한 것.

 

이제, 대전된 막대의 dx 에 해당하는 조각에 의해 P 에 형성되는 전기장을 구하는건 쉽다.

dx 를 점전하로 생각해도 좋다.

 

전하가 λ 의 선 전하 밀도로 균일하게 분포하고 있다고 했고, 길이가 dx 니까 원천전하에 해당하는 dq 는 우변의 형태가 된다.

 

길이 x 에 대한 적분이기 때문에 적분구간을 잘 설정해야 한다.

 

적분구간은 막대가 x 축의 어디부터 어디까지 존재하는지를 쓰면 된다.

그림이 자세해서 이해하기 아주 쉽고, 이제 남은 계산은 별거 없다.

 

 

피적분 함수를 올바르게 정하는게 중요하다.

 

 

 

[068-002] 원형 고리에 의해 형성되는 전기장

 

 

총 전하량 Q 가 균일하게 분포되어 있는 원형 고리에 의한 전기장을 구하는게 문제고, 관심있는 위치 P 는 고리의 중심과 같은 축에 있으며, 고리는 양으로 대전되어 있다.

 

앞의 문제와 가장 큰 차이는 전하가 얼마만큼의 비율로 분포되어 있는지 알려주지 않았다는 것.

λ 의 역할을 하는 값이 없다는 얘기다.

 

그래도 우리는 고리를 아주 작게 나눈다는 접근으로 시작해보자.

 

또, 선후의 문제지만 이렇게 대칭성이 있는 경우에는 전기장의 방향을 먼저 생각해보는것도 방법이다.

위 오른쪽 그림과 같이 위치 P 에서의 전기장은 x 축의 수직성분은 상쇄되고 x 축 방향 성분만 남게되는데, 이걸 바탕으로 dq 에 의해 발생하는 전기장을 구하면,

 

코사인은 그림에서 아래와 같이 정해지고,

 

이걸 위의 식에 대입하면,

 

이제 적분.

 

 

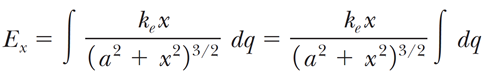
앞의 문제와 달리 전하 dq 로 부터의 거리를 변형해서 구하는 문제였고, 덕분에 적분구간을 생각 할 필요도 없었지만,

역시 피적분함수를 올바르게 구하는게 중요하다.

 

 

 

[068-003] 균일하게 대전된 원판에 의한 전기장

 

 

이번엔 면 전하 밀도 σ 로 대전된 원판에 의해 위치 P 에 형성되는 전기장을 구하는 문제다.

 

단위 면적 당 전하량이 면 전하 밀도니까, 위 식의 dq 는 다음의 형태가 된다.

 

이렇게 구한 dq 는 원판 그림의 진한 주황색 부분 (원형 고리) 의 전하량을 의미하고, 이 고리에 의한 전기장은 앞의 문제와 같이 x 축 방향 성분만 남게된다.

 

두번째 문제의 결과를 그대로 가져다 쓰면서 dq 만 바뀐다. 원형 고리에 의한 전기장 이니까 같은 결과를 얻는 것.

 

이제 적분.

 

이번엔 원판의 반지름 r 에 대한 적분이어서 적분구간을 고려해야한다.

 

 

주의할것은 문제를 보고 냅다 풀기 전에,

 

내가 가지고 있는 조건이 어떤건지 잘 확인하고, (형태만 알고 있는지, 밀도도 함께 알고 있는지와 같은..)

 

그 조건에서 피적분함수를 어떻게 만들 수 있는지,

 

그리고, 상쇄되는 성분은 없는지를

 

먼저 잘 파악하는게 중요하다.

 

 

여기까지.

 

 

 

[참고문헌]
주 교재 : Physics for Scientists and Engineers, 9th Edition, Serway/Jewett