앞서 병진운동을 다루면서, 운동(motion) 을 변화시키는 원인을 알아봤고, 그걸 힘(force) 이라 부르기로 했었다.
그럼, 회전운동의 변화를 야기하는건 무엇일까? 이게 토크다.
여닫이문을 여는 경우를 상상해보자. 물론, 교재에는 경첩 근처 특정 부위의 문짝 표면에 수직한 방향으로 F 만큼의 힘을 가하고 어쩌고.. 복잡한 얘기들이 있지만, 우리는 문을 여는 상황만 생각하자.
대신 문 손잡이를 잡고 여는 경우와 경첩 근처 (회전 중심 근처) 를 밀어서 여는 두 가지만 나눠서 생각하자. 당연히 문 손잡이를 잡고 미는 경우가 힘이 덜 든다.
우리는 상상에서, ‘힘’을 가해서 문의 ‘회전운동’을 발생 시켰는데, 이와 같이
임의의 축에 대해 물체의 회전을 발생시키는 힘의 경향을 측정한 양을 우리는 토크(torque) 라 부른다. 토크를 의미하는 기호는 그리스문자 ‘타우’ 이고, 아래와 같이 쓴다.

교재에는 이렇게 쓰여 있다.
“The tendency of a force to rotate an object about some axis is measured by a quantity called torque.”
힘에도 방향이 있고, 회전운동도 회전의 방향이 있으니, 토크도 벡터량 일 것이라 생각 할 수 있는데, 이번 단원에서는 그 크기만 고려하고, 벡터로서의 성질은 11장에서 다루기로 하자.
아래 그림과 같이 렌치로 볼트를 회전시키는 경우를 알아보자. 회전축은 볼트의 중심을 관통한다.

그림과 같은 방향으로 힘 F 가 가해지면, 토크의 크기는 다음으로 정의 된다.

r 은 회전 중심과 힘이 작용하는 위치 사이의 거리, d 는 회전축과 힘 F 의 작용선 (line of action) 사이의 거리이다.
위 그림에서 렌치를 대각선으로 갖는 아래쪽 큰 삼각형 (아래 그림을 봐도 됨) 에서

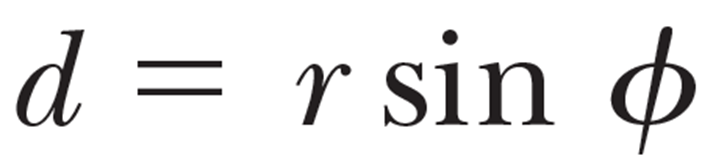
임을 알 수 있는데, d 를 힘 F 의 moment arm (또는 lever arm) 이라 부른다.
포인트는 작용하는 힘 중 회전운동의 반지름에 수직한 방향을 갖는 성분만이 회전운동에 영향을 준다는 것 이다.
언제나 그렇지만 운동이 복잡해지거나, 병진 운동과 같은 성질이 다른 운동이 복합적으로 발생하는 경우를 기술하려면 모멘트 암을 이용해 기술하는 것이 편해지지만,
우리는 회전운동뿐만 아니라 토크도 지금 처음 다루는거니까, 좀 더 편한 접근을 위해 반지름에 수직한 방향 이라는 표현을 사용했다.
힘 F 의 cos 성분은 그 작용선이 (line of action) 회전 중심을 지나므로, 축에 대한 회전운동을 야기하지 못한다.
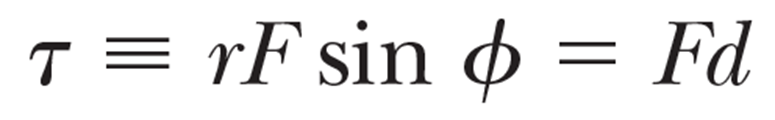
위 토크의 정의를 보면, 회전의 경향 (the rotating tendency) 은 힘 F 또는 d 가 커질수록 커짐을 알 수 있는데, 이는 앞에서 잠시 얘기한 여닫이 문을 여는 경우를 생각해보면 이해가 쉽다. 손잡이는 경첩에서 머니까 (d 가 크니까) 같은 힘으로 손잡이 부분을 미는 것이 경첩 부근을 미는 것 보다 문이 더 빠르게 회전하게 된다.
이제 둘 이상의 힘이 하나의 물체에 작용하면 어떻게 될지 알아보자.
시작은 아래 그림으로.

직관적으로, F1 은 반시계방향, F2 는 시계방향의 회전을 발생시킬 것 임을 알 수 있는데, 시계반대방향의 회전을 양(+), 시계방향의 회전을 음(-) 으로 약속했으니까 위 그림의 두 힘에 의해 발생하는 전체 토크 (net torque) 는 다음으로 쓸 수 있다.

쉽진 않지만, 토크와 힘을 잘 구분해야 한다.
힘은 뉴턴 법칙으로 기술이 가능한 병진운동의 변화를 발생시키는 원인이다.
물론 이 힘이 회전운동의 변화도 발생시키긴 하지만, 그 효과는 작용하는 힘의 크기와 모멘트 암에 의해 달라지며, 이 둘의 곱에 이름을 붙인게 토크다.
토크는 힘과 길이의 곱을 단위로 갖는데, SI 단위계에서 Nm (뉴턴 미터) 이다.
근데 이게 또 좀 그런게, 토크의 단위는 일(work) 의 단위와 같다. 물론, 힘을 주고 물체를 이동시키는 상황과 회전운동이 헷갈릴 일은 없겠지만..
이제 회전운동의 기본적인 내용들을 다뤘으니까, 다음에는 이 개념들이 실제 상황에 어떻게 적용되는지 알아보자.
[참고문헌]
주 교재 : Physics for Scientists and Engineers, 9th Edition, Serway/Jewett