[038-09-04]
이제 운동량 보존을 이용해서 어떤 상황을 분석하고 이해하는게 가능한지 알아볼텐데, 예를 들면 멈춰있는 무거운 볼링공에 탁구공을 집어 던지는 것 같은 상황에 대해서 알아보는 시간이다.
물론 결과는 알고있지. 볼링공은 아무일 없이 그냥 가만 있을테고, 탁구공은 (어떻게 방향이 잘 맞는다면) 내 얼굴로 튕겨올거다.
이게 과연 물리적으로 또 수식으로 어떻게 기술이 되며, 과연 현상과 동일한 결과를 얻을 수 있는지 알아보자.
충돌 (collision) 은 두 입자가 서로에게 가까워지다가 힘에 의한 상호작용을 하는 것을 의미한다. 는게 물리적 의미이긴 한데, 아원자입자에 대한 이야기가 심심치 않게 들리는 요즘에는 좀 그런 정의이긴 하다.
아래 그림의 b 와 같이 전기적으로 같은 성질을 갖는 미시세계의 입자 사이에는 “물리적인 접촉(physical contact)” 이 절대 일어나지 않기 때문이다.

하지만 우리는 앞에서 얘기한것처럼 볼링공과 탁구공 같은 큰 물체들에 관한 이야기를 할거다.
이제 위의 그림과 같은 상황으로 돌아와서, 서로 다른 질량을 갖는 두 입자가 충돌하면 충격력(impulsive forces)은 시간에 따라 복잡하게 변하겠지만, 이런 복잡함은 잊고 두 입자로 이루어진 고립계의 운동량이 보존된다는 사실만 가져가자.
운동량과 달리 운동 에너지는 충돌의 방식에 따라 보존이 될 수도 , 되지 않을 수도 있는데, 운동에너지의 보존 여부에 따라 우리는 그 충돌을 탄성(elastic) 또는 비탄성(inelastic) 으로 구분한다.
운동에너지가 보존되면 탄성충돌, 그렇지 않으면 비탄성충돌 이다.
두 입자의 탄성충돌 (elastic collision)은 충돌 전 후 계의 운동에너지가 동일한 충돌이다. 물론 운동량은 보존된다. 쉽게 접할 수 있는 경우는 당구공 끼리의 충돌인데, 약간의 변형이나 운동에너지의 손실이 발생하므로 어디까지 근사적인 (approximately) 의미의 탄성충돌이다.
당구장에서 눈을 감고 있어도 우리는 공끼리 충돌이 일어났다는걸 소리 만으로도 알 수 있을텐데, 이건 벌써 우리가 듣는 소리 만큼 충돌 과정에서 에너지의 변환이 발생했다는 얘기가 된다.
탄성충돌은 정의 상 에너지의 변환이 전혀 일어나지 않는 충돌이다.
비탄성충돌 (inelastic collision) 은 충돌 전 후 계의 운동에너지가 동일하지 않은 충돌이다.
비탄성충돌은 다시 (접두어가 없는) 그냥 비탄성충돌 과 완전 비탄성충돌 두 가지로 구분되는데,
고무공이 벽에 부딪히는 것과 같이, 충돌로 인해 운동 에너지의 일부가 변형 되거나 전이 되는 (transformed or transferred) 충돌을 비탄성충돌 이라 하고. 충돌 후 충돌한 물체가 한 덩어리가 되는경우를 완전 비탄성충돌 (perfectly inelastic) 이라 한다.
우리가 실제로 겪는 충돌들은 대부분 비탄성 충돌이다.
이제 아주 극단적인 두 충돌 – 완전 비탄성 충돌 과 탄성 충돌 – 을 운동량의 개념으로 어떻게 기술 하는지 알아보자.
완전 비탄성 충돌 (Perfectly inelastic collision)
완전 비탄성 충돌은 충돌 이후 충돌한 물체가 한 덩어리가 되는 경우이고, 그림으로 보면 다음과 같다.

앞의 설명 대로, 충돌이전 두 물체는 각각의 질량과 속도를 가지고 서로에게 직선으로 다가가고, 충돌이후 두 물체는 한 덩어리가 되어서 vf 의 속도로 움직인다.
고립계에서는 충돌의 양상에 관계없이 운동량이 보존되니까 우리는 충돌 전 두 물체의 전체 운동량과 충돌 후 하나가 된 물체의 운동량이 같음을 이용 할 수 있다.
자, 이 내용을 식으로 한번 써보자.
1. 운동량의 변화가 없다.
2. 충돌 전 후 운동량이 같다.
3. 충돌 전은 물체 두 개, 충돌 후는 한 개.

매우 간단.
탄성충돌 (Elastic collision)

완전 비탄성 충돌과 초기 상태는 같다. 두 물체가 서로를 향해 각자의 속도를 가지고 달려와서 부딪히고, 충돌 후에도 각자의 속도를 가지고 움직인다. 여기에 운동량과 운동에너지가 보존된다는 사실을 끼얹으면,

우리는 상황을 간단히 하기 위해서 두 물체가 정면으로 다가와서 충돌하는 경우를 생각하고 있으니까, 충돌 후 두 물체의 속도 벡터도 충돌 전과 동일한 직선 위에 있다고 생각 할 수 있다.
이렇게하면, 충돌 전과 후 속도벡터 네 개는 모두 동일한 직선위에 있게 되니까 오른쪽으로 움직이는 경우를 (+), 왼쪽으로 움직이는 경우를 (-) 로 단순하게 생각 하는게 가능해진다.
이제 운동에너지에 대한 두번째 식에 2를 곱해서 1/2 을 소거하고,
1번 물체에 대한 항과 2번 물체에 대한 항을 각각 모으면,

아주 간단한 인수분해를 하면,

여기까지를 얻고,
운동량 보존에 대한 식
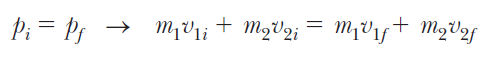
을 위와 마찬가지로 1번 물체에 대한 항, 2번 물체에 대한 항을 각각 모으고, 질량으로 묶으면,

이 관계를 얻는다.
이제 이렇게 얻은 두 식을 조합하고, 초기상태와 나중상태의 항 끼리 모으면,


짠.
두 물체의 충돌 전 상대속도와 충돌 후 상대속도는 크기가 같고 방향이 반대임을 알 수 있다.
이제 위의 관계와 운동량 보존에 대한 식을 조합하면 두 물체의 나중 속도를 구할 수 있는 관계를 다음과 같이 얻을 수 있다.

지금부터는 위의 나중속도에 관한 식을 가지고 얘길 좀 더 해보자.
충돌하는 두 물체의 질량이 같으면 무슨일이 생길까?
위 식의 m으로 쓴 부분이 모두 같아 진다는 얘기니까 다음의 관계가 얻어지는데,

두 물체의 나중속도는 반대편 물체의 처음속도와 같다. 조금 다르게 표현하면 속도의 교환이 일어난다.
정지 상태의 물체에 같은 질량을 갖는 물체가 와서 부딪히면, 정지 상태였던 물체는 날아온 물체와 같은 속도로 움직이고, 날아온 물체는 정지상태가 된다는 얘기다.
이게 말로 하면 되게 복잡한거 같지만, (요즘 친구들은 잘 안가는) 당구장에서는 쉽게 볼 수 있는 상황이다.
이제 다른 특수한 경우로, 두 물체의 질량이 다르고, 두번째 물체가 정지해 있는 상태인 경우를 생각해보자.
v2i=0 인 상황. 그러면 나중속도에 대한 위의 식은 아래와 같은 형태가 된다.

이제 여기에 움직이고 있는 물체1 의 질량이 정지 상태인 물체2 보다 아주 크다는 설정을 보태보자.
어떤 결과가 얻어질까?

이 결과를 말로 설명하면,
움직이고 있던 아주 무거운 물체1 은 충돌 후에도 속도 변화가 거의 없고,
정지상태였던 가벼운 물체2 는 충돌 후 물체1 의 2배 정도의 속도를 갖는다.
….. 생각해보면 아주 무서운 결과인데, 차가 사람을 치면 사람은 그냥 날아갈 수 밖에 없다.
이제 반대로,
정지상태인 물체2 의 질량이 움직이는 물체1 의 질량보다 아주 크면, 다음의 결과를 얻는데,


움직이던 가벼운 물체는 충돌 후 충돌 전의 반대 방향으로 움직이고, 정지상태였던 무거운 물체는 뭐 그냥 별일 없이 가만히 있을거라는 사실을 알 수 있다.
여기까지 충돌과 운동량에 대한 이야기를 했고,
볼링공에 탁구공을 던지면 벌어질 일을 수식으로 전개하고 설명하고 이해하는게 가능함을 알게 되었다.
1차원 충돌에 대한 이야기를 했으니까, 다음번엔 2차원 충돌에 대한 이야기를 하기로 하자.
그리고, 예전과 달리 당구에 대한 인식이 아주 좋아진 만큼, 어린친구들은 아빠한테 얘기해서 당구장을 견학삼아 가보도록 하자.
[참고문헌]
주 교재 : Physics for Scientists and Engineers, 9th Edition, Serway/Jewett
[계산과정 추가]

위의 관계가 어떤 과정으로 나오는지 궁금할 사람이 있을거 같아서 추가.
우리의 시작은 다음 두 식이었다.
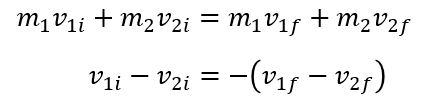
위 식에서,
알고있는건 파랑
구하고 싶은건 빨강
바꿔야 하는건 녹색
으로 색을 바꿔서 표시하면 식이 좀 알록달록 해 진다.

우리는 초기상태의 정보는 알고 있고, 두번째 물체의 최종속도는 필요가 없으니, 위의 식에 아래 관계를 대입하면,

이제 v1f 를 가진 항 만 두고 나머지 모든항을 옮기고, 정리하면,

이처럼,
모르는것을 알고있는것으로 표현하는 과정은 내가 알고있는게 무엇이고, 알고싶은게 무엇인지를 분명하게 아는 것이 그 시작이다.
'일반물리' 카테고리의 다른 글
| [040-09-06] 역학 : 질량중심 - The center of mass (0) | 2021.09.14 |
|---|---|
| [039-09-05] 역학 : 2차원 충돌 - Collisions in Two Dimensions (0) | 2021.09.01 |
| [037-09-03] 역학 : 선형 운동량과 충돌 : 운동량의 비고립계 적용 (0) | 2021.08.06 |
| [036-09-02] 역학 : 선형 운동량과 충돌 : 운동량의 고립계 적용 (0) | 2021.08.02 |
| [035-09-01] 역학 : 선형 운동량과 충돌 : 선형 운동량 (Linear momentum) (0) | 2021.07.30 |