[034]
앞에서 시스템에 에너지가 저장되는 세 가지 방식 - 운동에너지, 포텐셜 에너지, 내부에너지 - 을 알아봤다. 이번에는 고립계와 비 고립계 (isolated and nonisolated systems) 두 가지 유형의 시스템에 대한 에너지 관점의 설명을 통해 에너지 보존에 대한 이야기를 해 보자.
이름에서 알 수 있듯, 고립계와 비 고립계의 가장 큰 차이는 계가 주변 환경과 에너지 교환이 가능한가의 여부이고, 이 때문에 두 시스템의 에너지가 변환되는 방식의 차이가 발생하는데, 이런 상황들을 어떻게 기술 할 수 있는가에 대한 이야기가 될거다.
계의 경계를 지나 교환되거나 전달되는 에너지의 비율을 일률 (Power) 이라는 개념으로 다루는 방법도 알아보자.
[034-01] 비 고립계 - Nonisolated system
입자(물체)에 힘이 작용하면 입자의 운동에너지의 변화가 생기고, 이 변화를 일-운동에너지 정리로 기술 할 수 있음을 앞에서 알아봤다. 여기서 입자를 하나의 계로 설정하면, 이 상황은 비 고립계의 아주 좋은 예가 되고, 계와 환경의 상호작용에 의해 에너지의 전달이 일어났다고 설명 할 수 있다. 이와 달리, 시스템이 속해있는 환경과 상호작용을 하지 않으면, 고립계로 취급하여 기술 할 수 있다.
앞에서, 시스템으로 에너지가 전달되는 한가지 방식으로 일(work)을 다뤘는데, 여기서는 일 외에 시스템으로 에너지가 전달되거나, 시스템에서 외부로 에너지가 전달되는 또 다른 방식에는 어떤게 있는지 알아보자.
일 (Work) : 계에 변위를 발생시키는 힘을 작용하여 에너지를 전달
역학적 파동 (Mechanical waves) : 공기나 물 같은 매질을 통해 전파되는 소란 (disturbavce) 으로 에너지를 전달. 지진파나 바다의 파도, 소리 등을 포함하는 개념. 교재의 16~18장에서 다룸.
열 (Heat) : 계와 환경의 온도 차이에 의해 발생하는 에너지의 전달. 높은 온도는 계를 구성하는 원자나 전자의 속도를 빠르게 하고, 이렇게 빨라진 입자들은 주변의 속도가 느린 입자와 충돌하여 에너지를 전달. 이러한 과정으로 게의 내부 에너지가 증가. 교재의 20장에서 다룸.
물질 전달 (Matter transfer) : 에너지를 가진 입자가 계의 경계를 지나 유입되거나 빠져나가는 현상. 대류라 부르는, 뜨거운 공기가 공간을 채우는 과정이나 자동차에 연료를 채우는 것 같은 행동을 포함. 20장에서 다룸.
전기,전력 전송 (Electrical transmission) : 전류 (electric current) 에 의한 에너지의 전달. 드라이어에서 뜨거운 바람이 나오거나, 냉장고의 음식이 차갑게 유지되는 등. 27,28 장에서 다룸.
전자기 복사 (Electromagnetic radiation) : 빛과 같은 전자기 파동에 의한 에너지의 전달. 태양에서 지구로 우주 공간을 지나 에너지가 전달되거나, 전자레인지로 음식이 데워지는 현상 등. 34장에서 다룸.
힘과 일에 대한 이야기 다음에 계와 계에서 일어나는 현상을 다루면서 에너지의 개념을 도입했는데, 현상을 에너지로 기술하는 가장 큰 이유가 바로 에너지 보존 때문이다. 에너지는 새로 생성되거나 소멸하지 않고, 보존된다는 것이 에너지 보존이다.
에너지가 보존된다는 사실은 아주 다양한 장르의 수 많은 실험을 통해 검증되었으며, 아직까지 에너지가 보존되지 않는 경우는 없었다. 에너지가 보존된다는 사실을 바탕으로 우리는 다음과 같은 이야기를 할 수 있다.
계의 총 에너지가 달라졌다면, 위에 나열한 방식 중 한 가지 방식으로 계의 경계를 지나 에너지가 이동했다고 생각 할 수 있다.
if the total amount of energy in a system changes, it can only be because energy has crossed the boundary of the system by a transfer mechanism such as one of the methods listed above.
힘이나 속도는 보존법칙을 따르지 않는 물리량인데, 교재의 설명을 따라 보존된다는 것 과 보존되지 않는다는 것의 차이를 생각해보자.
은행 계좌에 들어있는 돈은 보존되는 양 이다. 계좌에 들어있는 돈은 계좌의 외부에서 더 넣거나, 계좌로부터 꺼내지 않으면 즉, 계좌의 경계를 지나는 돈의 흐름이 발생하지 않으면 같은 양이 유지된다.
이와달리, 인구는 보존되지 않는 양 인데, 국경을 건너는 사람들은 물론 인구의 증감에 영향을 미치지만, 국가 내부에서 태어나거나 죽는 사람의 숫자도 인구에 영향을 미친다. 근데, 죽거나 태어나는 사람들은 국경을 건너는 이동을 하지 않고도 인구에 영향을 미치는 것 이다.
물론, 에너지는 탄생이나 소멸의 개념을 갖지 않는다.
에너지 보존을 간단한 수식으로 쓰면 다음과 같은데,

계의 에너지 변화량 은 계의 경계를 지나 이동한 에너지의 합 과 같다.
위 식을 좀 자세히 써 보면,

이렇게 복잡해 보이는 식이 되는데, 왼쪽은 계의 에너지 변화를 좀 자세히 쓴 거고, 오른쪽은 계와 외부의 발생 가능한 상호작용을 쓴 것이다.
우변의 항목을 순서대로 쓰면, 일(work), 열(heat), mechanical wave, matter transfer, electrical transmission, electromagnetic radiation 이다.
물론 다루고자 하는 특정 상황들에선 우변의 항목 대부분이 0 이 되고 식은 간단한 형태가 되는데, 아주 특별하게, 우변의 모든 항이 0 이 되는 계를 곧 다룰 고립계 (isolated system) 라 부른다. 고립계는 외부와의 상호작용을 하지 않는 계 인 것이다.
임의의 비고립계에 힘이 인가되고, 그 힘의 작용으로 계의 속력의 변화만 발생했다면, 에너지의 전달은 앞에서 다룬 일(Work) 의 형태로 발생했고, 그 결과로 계의 운동에너지만 변화 했으므로, 위 에너지 보존의 식은,
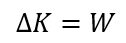
의 형태가 되는데, 이는 앞에서 다룬 일-에너지 정리와 같은 형태가 된다. 일-에너지 정리는 에너지보존의 한가지 경우인것이다.
[034-02] 고립계 - Isolated system
물리에서 가장 일반적으로 다루는 상황이 고립계인데, 어떠한 방식으로도 계의 경계를 지나는 에너지 교환이 일어나지 않는 계에 대한 이야기이다.
말이 좀 어려운거 같지만, 또 알고보면 그렇지도 않으니까.. 중력이 존재하는, 책과 지구 둘로 이루어진 계에 대한 이야기로 시작해보자.

위 그림의 빨간 화살표 반대 방향으로 책을 들어 올리면, 중력 포텐셜 에너지 (gravitational potential energy) 가 계에 저장 (stored) 된다. - 보신분들은 아시겠지만, 원래 이렇게 영어 단어를 갖다 쓰는걸 좋아하지 않는데, "저장" 이라는 단어에 혹여 오해가 있을까봐 교재의 표현을 가져왔다.- 그리고 저장된 중력 포텐셜 에너지의 크기는 외부에서 계에 해 준 일의 크기를 계산하여 구할 수 있다.

책을 들어 올리는, 즉 계의 외부에서 해 준 일의 크기는 일단 잊고, 들어올려진 책이 원래 위치로 떨어지는 상황을 고려해보자.
책이 들어올려진 높이 -초기위치, yi- 에서 떨어진 후 위치 -최종위치, yf- 로 떨어지는 동안 중력이 한 일은

앞에서 다룬 일-에너지 정리로 부터 책에 해 준 일은 책의 운동에너지와 같다는 사실을 위 식과 연결시키면,

즉, 책의 운동에너지의 변화량은 중력이 책에 해 준 일의 크기와 같다.
이제 이 이야기를 책과 지구로 이루어진 계의 관점으로 옮겨보자.
우변 - 중력이 책에 한 일 - 은 계의 포텐셜 에너지의 변화량이고, 다음으로 쓸 수 있다.

책을 들어올리는 일이 포텐셜의 증가를 의미하므로, 책이 떨어지는 과정은 계가 가진 포텐셜 에너지의 감소로 표현된다.
책-지구 계에서 책은 운동이 가능한 단 하나의 구성요소 이므로, 좌변 - 책의 운동에너지 변화량 - 은 계 전체의 운동에너지 변화량으로 취급 할 수 있다. 이걸 식으로 쓰면,

위 두 식을 결합하면 최종적으로 다음의 관계를 얻게 되는데,

계의 포텐셜 에너지가 감소한 만큼 운동에너지는 증가한다.
포텐셜 에너지 변화량을 좌변으로 이항하면, 다음을 얻는데,

이 식의 좌변은 계에 저장된 (stored) 에너지 변화량의 총 합을 의미하고, 우변의 0 은 계의 좌변의 에너지 변화가 발생하는 동안 계의 경계를 지나는 에너지 교환이 없음을 의미한다.
좀 더 자세히 쓰면,
식의 좌변은 우리가 책-지구 둘 로만 이루어진 계를 설정했고, 지구의 중력이 책의 위치를 변화시키면서 한 일의 크기와 우리가 관심있는 계의 구성요소 중 운동이 가능한 단 하나의 물체인 책의 운동에너지 변화 사이의 관계를 의미하고,
우변은 그 과정에서 책-지구 둘 외의 물체나 힘이 가해지지 않았다는 사실을 의미하고, 이는 곧 우리가 관심있는 계가 주변 환경으로부터 고립되어있음 (isolated) 을 의미한다.
우리는 고립계에 대한 이야기를 중력장에 대한 이야기에서 발전시켰지만, 모든 유형의 포텐셜 에너지를 갖는 계에 대해서도 같은 이야기를 할 수 있으며, 이 사실을 다음의 한 마디로 쓸 수 있다.
고립계에서는 계의 포텐셜 에너지의 변화량과 운동 에너지 변화량의 합이 0 이다.

이전 이야기에서 우리는 계의 운동에너지와 포텐셜 에너지의 합을 계의 역학적 에너지로 정의 했는데, 고립계로 간주하는 경우, 이 이야기들은 계의 역학적 에너지가 보존됨을 의미한다. 즉, 역학적 에너지의 변화량은 0 이다.


위 식은 책에는 없는데, 설명과 수식이 연결이 되지 않을까봐 추가했다.
역학적 에너지의 변화량은 곧 계의 운동에너지와 포텐셜 에너지의 변화를 의미하는데, 고립계에서 이 둘은 독립적으로 변화하지 않음을 지금까지의 논의로 알게됐으니, 즉, 한쪽이 변하면 그와 동일한 크기로 반대쪽도 변하니, 계의 역학적 에너지의 변화량이 0 이 된다는 말이다.
마지막으로 위 식을, 비보존력이 작용하지 않는 고립계의 역학적 에너지 보존 (conservation of mechanical energy) 이라 부른다.
이번에는 위에서 얻은 에너지 변화량의 합이 0 이라는 식을 다음으로 변형해보자.

위 식은 "처음상태의 역학적 에너지와 최종상태의 역학적 에너지의 크기가 같다." 는 의미인데, 이를 책이 떨어지는 상황에 적용해보면,
책-지구 로 이루어진 계의 포텐셜 에너지는 감소하고, 운동에너지는 증가하며, 이 두 형태의 에너지의 합은 일정하게 유지된다. 는 설명을 얻을 수 있다.
만약 고립계에 비보존력이 작용하면, 역학적 에너지는 보존되지 않더라도 계의 전체 에너지는 보존되는데, 이를 계의 에너지 보존 이라 하며, 다음의 식으로 쓸 수 있다.

여기서 계의 에너지 (Esystem) 는 계가 갖는 운동, 포텐셜, 내부 에너지를 비롯한 모든 형태의 에너지를 포함하며, 이 식이 고립계의 에너지를 설명하는 가장 일반적인 형태이다.
마지막으로, 위 식은 앞에서 다룬 식

의 우변의 모든 항이 0 임을 의미한다.
** 이 사이에 교재의 섹션 8.3 운동 마찰과 관계된 현상 (Situations involving kinetic friction) 이 있는데, 왠지 흐름에서 약간 벗어난 느낌이 들어서 생략했다. 아주 기본적인 벡터 연산을 해야하는 식들이 좀 있기도 하고..
다음 섹션에서 이 운동 마찰력에 의한 에너지 변화를 가지고 이야기를 진행하는데, 마찰에 대해서 먼저 다루지 않은게 의아 할 수도 있을거 같긴 하지만 일단 생략 하고 진행하기로 한다.
혹시 궁금하신 분은 교재의 섹션 8.3을 보시면 되고, 요청이 있으면 따로 올리도록 하겠다.
[034-03] 비보존력에 의한 역학적 에너지의 변화 - Changes in mechanical energy for nonconservative forces
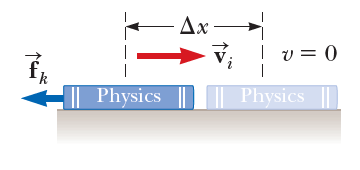
위 그림과 같이 책이 미끄러져 움직이는 상황을 생각해보자.
수평방향의 힘은 운동마찰력 밖에 없고, 책이 움직인 거리가 d 라면, 이 힘은 -fkd 의 크기를 갖는 운동 에너지로 변환된다. 이 과정은 계의 에너지에 관한 이야기에서 다룬 아래의 식과

생략한 섹션 8.3 에서 얻어진 다음의 식

을 통해 이해 할 수 있다.
좌변의 W other forces 는 책을 움직이게 하는 마찰 이외의 모든 힘에 의한 일 이고, fkd 는 운동 마찰에너지에 의한 일 을 나타낸다.
이제 이 책이 포텐셜 에너지의 변화를 표현 할 수 있는 (exhibit) 계의 일부라고 생각해보자. 그러면, -fkd 라는 값은 운동 마찰력에 의해 발생한 계의 역학적 에너지의 변화량을 의미하게 된다.
예를들어, 마찰이 있는 빗면을 따라 흘러내리는 책의 경우, 책-지구 계의 운동에너지와 중력 포텐셜 에너지는 책이 미끄러지는 동안 다음의 방식으로 변하게 된다.

계의 역학적 에너지의 변화량은 계의 운동에너지와 포텐셜 에너지 각각의 변화량의 합이고, 이는 빗면을 따라 내려오는 책의 운동 마찰력에 의해 발생한 일의 크기와 같고, 이는 계의 내부에너지의 변화와 같고... 말이 기네..
여튼, 책을 움직이게 하는 모든 힘이 한 일에서 마찰에 의해 상쇄되는 일의 크기를 빼고 난 나머지는 계의 운동에너지 변화로 나타난다.
일반적으로 고립계에 비보존력이 작용하면, 다음이 성립한다.

이 식의 좌변은 위에서 다룬 다음의 식과 같은데,

고립계에 비보존력이 작용하는 경우 역시 계의 경계를 통과하는 에너지의 전달이 없는 상황으로 볼 수 있다.
비보존력이 작용하는 계가 외부의 영향을 받는 비 고립계라면,
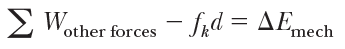
모든 힘 들에 의해 발생한 일 및 운동 마찰력에 의한 일은 계의 역학적 에너지의 변화를 일으키고, 이를 다음의 두 식과 연결하면,

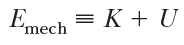
다음의 결과를 얻게된다.

교재에는 위 식이 비보존력이 작용하는, 포텐셜 에너지를 갖는 비고립계 모델을 의미한다고 설명하고 있는데, 좀 쉽게 말하자면,
우리가 어떤 계에 어떤 방식으로든 일을 해주면, 그 일은 사라지지 않고, 계의 운동에너지, 포텐셜 에너지, 내부에너지의 변화로 "모두" 변환된다 는 의미이고, 이것은 곧 에너지가 보존됨을 의미한다.
[034-04] 일률 - Power
교재에서 일률은 7장의 문제 (예제 7.7) 로 이야기를 시작하는데, 우리는 문제풀이는 하고 있지 않으니까, 어떤 문제인지 부터 알아보자.


그림의 남자가 일정한 각도를 갖는 경사면을 이용해 냉장고를 트럭에 실을려고 하는데, 경사면의 길이 L 을 길게하면 본인이 해야하는 일의 크기가 줄어드는걸로 믿고 있댄다. 이게 맞는 생각이냐?
라는게 7장의 문제이고, 우리는 이 상황으로 일률에 대한 이야기를 시작해보자.
뭐 이런저런 얘기를 길게 할것도 없이, 우리는 남자가 해야하는 일의 크기가 경사로의 길이와는 관계 없이 일정하다는걸 알고있고, 그 크기는 중력에 대해 냉장고를 원하는 높이까지 올려야 하는 일의 크기를 구하면 알 수 있다.
저 남자가 본인의 믿음대로 경사로의 길이를 길게 설치해서 냉장고를 트럭에 실으면, 짧은 경사로를 이용하는 사람보다 트럭에 냉장고를 싣는데 더 많은 시간이 필요하게 된다. 물론 일의 크기는 같고.
이 내용을 바탕으로 우리는 순간일률 (Instantaneous Power : P) 을 에너지 전달 (transfer) 의 시간에 따른 비율 로 정의하고, 이를 다음과 같은 식으로 쓸 수 있다.

지금 우리는 일 (Work) 을 에너지 전달의 방식 (the energy transfer method) 의 개념으로 다루고 있고, 일에 대한 이러한 접근 방식은 앞에서 다룬 모든 형태의 에너지 전달에 적용 할 수 있다.
물체에 외력이 작용하고, 이 힘이 시간 간격 △t 동안 물체에 W 만큼의 일을 했다면, 이 시간 간격동안 평균 일률 (Average Power) 은 다음으로 쓸 수 있다.

따라서, 이미 우리가 알고있는대로 경사로의 길이에 관계없이 남자가 해야하는 일의 크기는 일정하지만, 긴 경사로를 이용하는 경우의 일률은 더 작아진다.
속도, 가속도를 정의 할 때와 같이 순간일률은 평균일률에 시간간격 △t 가 0으로 가는 극한을 취해서 얻어지는 극한값이다.

일에 대한 이전 이야기에서 일의 무한소 (infinitesimal) 성분을 다음과 같이 구할 수 있음을 알아봤고,
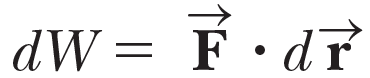
이를 이용해 일률(순간일률) 을 다시 쓰면 다음과 같다.

SI 단위계에서 일률의 단위는 Joules per second (J/s) 이고, 이는 전기에서 많이 사용하는 단위인 와트 (Watt : W) 와 같다. 이 관계는,
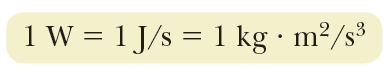
또, 일률은 마력 (horsepower : hp) 와 다음의 관계가 있다.

이제, 에너지 (또는 일) 를 일률을 단위를 이용해서도 쓸 수 있는데, 1kWh (1킬로 와트 시) 는 1시간 동안 1kW 의 비율 (초당 1,000J 의 비율) 로 에너지가 전달되었음을 의미하고, 이 관계를 식으로 쓰면 다음과 같다.

kW 는 일률의 단위, 여기에 시간이 곱해진 kWh 는 에너지의 단위임을 구분 할 수 있으면 된다.
우리가 매달 내는 전기세는 고지서에 적힌 기간동안 전기전송을 통해 가정으로 전달되고 사용된 에너지의 크기에 대한 값을 지불하는 것이다.
예를 들어,
100W (0.1kW) 용량의 전구를 1시간동안 켰다면, 전구가 사용한 에너지의 크기는 일률과 시간의 곱인 0.1kWh 가 되고, 이를 줄로 환산하면,

위와 같은 방식으로 집에서 사용하는 가전제품의 전력량을 계산 할 수 있다.
[참고문헌]
주 교재 : Physics for Scientists and Engineers, 9th Edition, Serway/Jewett
'일반물리' 카테고리의 다른 글
| [036-09-02] 역학 : 선형 운동량과 충돌 : 운동량의 고립계 적용 (0) | 2021.08.02 |
|---|---|
| [035-09-01] 역학 : 선형 운동량과 충돌 : 선형 운동량 (Linear momentum) (0) | 2021.07.30 |
| [033] 역학 : 계의 에너지 - Mechanics : Energy of a System (2) | 2020.07.16 |
| [032] 역학 : 회전운동과 뉴턴법칙의 응용 - Mechanics : Circular motion and other applications of Newton's laws (0) | 2020.06.24 |
| [031.5] 등속원운동과 주기 운동 - Uniform circular motion & Periodic motion (0) | 2020.06.16 |