[033]
지금까지 힘과 운동 그리고 뉴턴의 운동법칙과 그 의미를 알아봤고, 이를 바탕으로 물체의 운동을 어떻게 해석 할 수 있는지 알아봤다. 이번에는 계의 에너지에 대한 이야기를 해 볼텐데, 아무래도 우리가 일상적으로 사용하는 '에너지' 라는 단어의 의미와는 좀 다른 개념이 필요한 이야기가 될 것으로 생각된다.
에너지는 아주 다양한 형태로 존재하는데, 우리 주변에서 일어나는 모든 물리적 현상은 에너지와 에너지의 전달과 에너지의 변형 (transformation) 과 관련되어있다. 말 그대로 '모든' 현상이 에너지와 관련되어 있는데, 정작 우리에게 '에너지' 자체에 대한 정의나 개념은 상당히 추상적인게 사실이다. 누가 '에너지가 대체 뭐냐?' 라고 묻는다면 뭐라고 대답 할 수 있을까?
물을 부은 냄비를 가열하면 물의 온도가 올라가고 어느순간부터는 물이 끓기 시작한다. 충전된 전기를 모두 사용하면 휴대폰은 더 이상 아무런 동작도 하지 않는다. 이는 각각 열에너지, 전기에너지와 관련된 현상인걸 우리는 알고 있는데, 둘은 전혀 다른거 같은데 왜 에너지라는 단어를 같이 사용하는걸까? 그럼 물체를 움직이게 하는 힘은 에너지와 관련이 없는걸까? 나아가, 앞에서 힘과 물체의 운동에 대한 이야기를 에너지라는 개념을 이용해서 설명할수는 없을까?
이런 질문들에 어떤 대답을 다루는게 이번 글의 내용이다.
챕터 단위로 작성하다 보니, 이번 내용도 길어질거 같아서, 순서를 먼저 정리하고 시작하자.
- 계와 환경
- 일정한 힘이 한 일
- 두 벡터의 내적
- 변하는 힘이 한 일
- 운동에너지와 일-운동에너지 정리
- 계의 포텐셜 에너지
- 보존력과 비보존력
[033-01] 계와 환경 - Systems and environments
계 모델 (system model) 은 에너지를 바탕으로 현상을 설명하는데 사용되는 개념이다. 힘과 운동에 대한 이야기에서는 우리가 관심있는 물체나 입자에 작용하는 힘들을 하나하나 구분했던것과 달리, 계 모델 에서는 우주의 아주 작은 부분에 관심을 두고, 그 외의 공간은 무시하는 방식으로 현상을 설명할거다. 여기서 우리가 관심을 가지고 있는 우주의 아주 작은 부분을 계 (system) 라고 한다.
아직은 익숙치 않지만, 이런 접근은 앞에서 물체에 작용하는 힘 중에 우리가 관심있는 힘만 적용해서 현상을 설명했던것과 같은 방식이다. (물론 그 힘들이 작용하지 않는다는게 아니다.)
현상을 계로 이해하고 기술하는 첫번째 단계는 우리가 관심있는 계를 명확히 하는 일인데 (identifying the system), 다음의 경우들을 하나의 계로 간주 할 수 있다.
1) 하나의 입자나 물체, 2) 입자나 물체의 집합체, 3) 특정한 현상이 일어나는 공간 (예: 자동차 엔진의 실린더 내부), 4) 크기와 형태가 시간에 따라 변하는 경우 (벽에 부딪힐때 모양이 변하는 고무공)
쉽게 말하면, 모든 물리적 현상을 계의 개념으로 설명 할 수 있다는 말이고, 좀 구체적인 예를 들자면, 가열되고 있는 냄비 내부를 하나의 계로 취급하여 접근하고 해석하는게 가능하다는 이야기이다. (안에는 물과 수증기와 각종 기체 분자와 물속의 이물질과 뭐 별게 다 들어 있겠지만..)
또 다른 예로, 아무것도 없는 공간에 있는 네모난 상자를 상상해보자. 이 네모난 상자 자체가 하나의 계가 될 수 있고, 상자의 표면은 계의 경계가 된다. 만약 외부로부터 상자에 힘이 가해진다면, 이 힘을 계의 환경 (environment) 에서 계의 경계를 통해 계에 영향을 미치는 것으로 생각 할 수 있고, 이와 같은 방법으로 현상을 해석하는 것이 이번 이야기에서 다룰 내용이다.
대충 생각해도 계가 환경으로부터 영향을 받을 수 있는 방법이 엄청나게 많기 때문에, 모든 상황에 대한 설명을 하나하나 하는건 불가능하니까, 우리는 일 (work) 이 무엇인지에 대해 먼저 알아보자.
[033-02] 일정한 크기의 힘이 한 일
일 (Work) 은 우리가 일상적으로 사용하는 의미와 물리에서 사용하는 의미 사이에 분명한 차이가 있는 단어이고, 일과 에너지에 대한 이야기는 모두 벡터를 이용해서 진행 할 수 밖에 없는데, 이는 책상에 놓여있는 지우개를 눌러보고 밀어보는 것 만으로도 왜 그런지 이해가 된다.
손가락으로 지우개를 위에서 수직으로 '누르면' 움직이지 않지만, 그보다 약한 힘으로 비스듬히 '밀면' 누를때보다 적은 힘으로 지우개를 움직이게 할 수 있다. 즉, 우리가 어떤 계(지우개)에 작용한 힘의 효과를 이해하고 설명하기 위해서 힘을 벡터로 이해하고 표현하는 과정은 필수적이다.
책상의 지우개를 밀 때, 지우개가 같은 거리를 이동하는데 어느만큼의 힘이 작용 했는지만이 아니라 지우개가 결국 어느만큼의 거리를 이동했는지도 물론 상황을 설명하는데 아주 중요한 사항이 될거다. 크기와 방향과 이동거리가 모두 중요하다는 말.
이렇게 물체에 (계에) 일정한 크기와 방향을 갖는 힘이 작용해서 물체가 직선으로 움직인 경우를 그림으로 그려보면 다음과 같다.

이 상황을 바탕으로 물리에서 말하는 일을 정의 할 수 있는데,
The work W done on a system by an agent exerting a constant force on the system is the product of the magnitude F of the force, the magnitude △r of the displacement of the point of application of the force, and cos u, where u is the angle between the force and displacement vectors:
계에 작용하는 일정한 힘이 계에 한 일은 힘의 크기 (F), 물체의 (계의) 변위 (△r), cos θ 의 곱으로 정의되며, θ 는 힘 벡터와 변위 벡터 사이의 각도이다.

위 표현으로 알 수 있듯, 벡터로 표현되는 힘이 한 일은 스칼라여서 방향 없이 크기만 갖는 양 이다. 물론 여기서 의자를 가만히 들고 있는건 힘만 들지 아무일도 하지 않은 것 이라는 정말 잊고싶은 말 같지도 않는 농담이 자꾸 생각나지만, 우리는 이런건 농담이라고 생각하지 말자.
그저 물리에서는 일을 저렇게 정의 해서 사용하고 있고, 힘이 작용하지 않았거나, 물체가 이동하지 않았거나 (변위이다), 힘이 물체의 이동방향에 수직으로 작용했다면, 그 힘이 한 일은 0 이라는 아주 건조한 의미만 갖고 있을 뿐 이다.
일은 스칼라이지만 물론 양,음의 부호는 가질 수 있는데, 이 부호는 변위의 방향 대한 힘의 방향으로 정해진다. 즉, 위 식의 F 와 cos θ 의 곱으로 일의 부호가 정해지게 되는데, 힘의 크기는 항상 양수일테니, 사실 일의 부호를 결정하는건 cos θ 라고 봐도 된다.
결국 저 식이 말하고자 하는 바를 좀 쉽게 이해하자면, 물체에 작용한 힘이 물체가 움직인 방향으로 어느만큼의 영향을 미쳤느냐는 것이고, 그 효과를 수치화 한 것을 일이라 하자는 것이다. 그럼 힘을 구성하는 다른 방향 성분들의 효과는? 그 힘들도 어떻게든 물체의 운동에 영향을 미쳤을 수 있지만, 여기서는 관심 없다.
일의 단위를 알아보자. SI 단위계에서 힘은 뉴턴[N]을 단위로 갖고, 길이 (변위) 는 미터[m]를 단위로 가지니까 자연스럽게 일은 뉴턴미터[N·m] 를 단위로 갖는데, 두 단위의 곱을 우리는 줄[J] 로 쓴다.
현상을 계(system) 의 관점으로 다루면서 가장 중요한 것은 일이 곧 에너지의 전달 이라는 것이다. 계에 한 일이 존재하고, 그 값이 양수라면, 에너지가 계로(to the system) 전달 된 것 이고, 음수라면 계에서(from the system) 에너지가 전달 된 것이다. 만약 계가 주변 환경과 상호작용 한다면, 이러한 에너지의 전달은 계가 갖고 있는 에너지가 늘어나고 줄어드는 형태로 발생하게 된다.
[033-03] 벡터의 내적 - The scalar product of two vectors
여기서는 벡터의 내적이 무엇을 의미하는지만 말하고, 계산에 대한 다양한 내용은 넘어갈 생각이다.
숫자에 사칙연산이 있듯, 방향과 크기를 갖는 벡터 사이의 계산에도 일정한 규칙이 있는데, 그 중 하나가 '내적'이고, 영어로는 스칼라 곱 (scalar product) 이다. 내적은 두 벡터가 만드는 사각형 (보통 평행 사변형) 의 넓이를 의미하는데, 나에게는 스칼라 곱 이라는 단어가 받아들이기 편했다. 크기와 방향을 갖는 두 벡터를 약속된 규칙으로 계산하면 방향 없이 크기만 갖는 값으로 바뀐다. 그리고 계산 결과가 스칼라량 이기 때문에 스칼라 곱 이라는 이름이 붙었다.
앞의 일에 대한 이야기에서 다룬 것 처럼, 이 값은 힘이 계에 한 일을 설명 할 수 있고, 힘이 계의 운동에 기여한 정도를 크기로 나타낸 값이다.

두 벡터의 내적의 값은 위와 같이 두 벡터의 크기와 사잇각의 코사인 값을 곱해서 얻을 수 있다.
[033-04] 변하는 힘이 한 일
이제 계에 작용하는 힘이 위치에 따라 달라지는 경우를 생각해보자. 힘이 달라지는다는 말은 힘의 크기와 방향이 모두 달라진다는 의미이지만, 여기서는 문제를 간단히 하기 위해 물체의 위치와 힘의 방향을 x 축 방향으로 제한하여 생각하자. 그러면 힘의 크기만 달라진다고 생각하면 된다.
"힘이 위치에 따라 다른" 상황을 그래프로 나타내면,
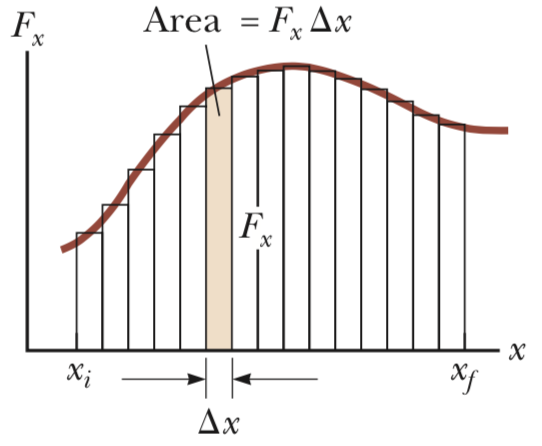
xi 는 물체의 처음 위치, xf 는 물체의 최종 위치를 의미하고, 그림의 색칠된 부분처럼 아주 작은 거리 (△x) 를 움직이는 동안 Fx 의 힘이 작용 했다면, 그 동안 힘이 한 일은 Fx 와 △x 의 곱으로 표현된다. 여기에 미분의 개념을 도입해 △x 를 아주 작게 만들고, 이 값들을 처음위치부터 최종위치까지 모두 더하면 힘이 계에 한 일의 대략적인 값은 다음이 된다.
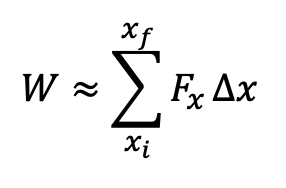
아직 일의 크기는 근사값 (approximate value) 인데, 위의 관계에 △x 가 0으로 가는 극한을 취하면, 일의 적분 표현을 얻을 수 있고, 이는 실제 힘이 계에 한 일의 정확한 값이 된다.

그리고 이 표현을 위의 그래프에 나타내면 다음과 같은데, 곡선 아래의 넓이를 의미한다.
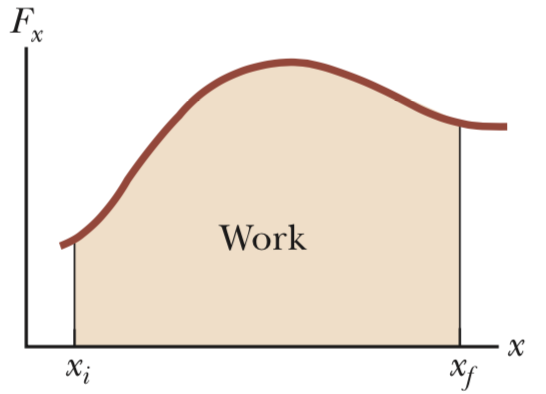
적분 기호 (integral) 가 극한 (limit) 과 합의 기호 (sigma) 의 결합이라는 내용에 힘과 변위에 대한 물리적 의미가 보태지면 일이 되고, 이는 힘과 위치의 그래프에서 곡선으로 둘러싸인 부분의 넓이를 함께 의미한다.
[033-05] 운동에너지와 일-운동에너지 정리
여기까지 이야기에서 일은 계로 에너지가 전달되는 과정이며, 환경이 계에 영향을 미치는 것이라는 사실을 이해하고 수학적인 표현은 어떻게 되는지 알아봤다. 이제 환경이 계에 미친 영향의 결과가 어떤 현상으로 발생하는지 알아보자.
힘이 계에 한 일은 계에 에너지를 전달하고, 이에 의해 계의 속력이 변하는 상황은 비교적 이해하기 쉬운 에너지 전달의 예가 될 수 있고, 이러한 형태의 에너지를 운동에너지 (kinetic energy) 라고 한다.

위와 같이 질량 m인 물체(계)에 외부에서 힘이 가해져서 물체의 위치와 속도가 변하는 상황을 생각해보자. 앞에서 얻은 일의 적분형 표현을 이 상황에 맞게 고쳐쓰면,

아래첨자로 쓴 "ext"는 external 의 첫 세 글자이고, 외부에서 작용한 일이 한 일 이라는 의미이다. 이 식의 우변을 아래 순서로 바꿔쓰면,
1. 뉴턴의 두번째 법칙에 따라 적분기호 안의 합력은 물체의 질량과 힘에 의해 물체가 갖게된 가속도로 바꿔쓰고,
2. 가속도를 시간에 대한 속력의 변화로 바꾸고,
3. chain rule (연쇄법칙) 로 적분변수를 dx 에서 dv 로 바꿔주고,
4. 적분 구간을 위치에서 속력으로 바꾸면,

힘이 한 일이 특정한 값 (1/2 m v^2) 과 관련이 있다는 결론을 얻게되는데, 이게 여러모로 중요한 의미를 갖는 양 이어서 물리에서는 따로 운동에너지 (Kinetic Energy) 라는 이름을 붙이게 된다.
에너지를 정의 할 때, 에너지의 단위가 [Nm] 임을 알았다. 운동에너지도 "에너지" 가 붙으면 같은 단위를 가져야 할테니 한번 확인해보자.
질량은 [kg], 속력은 [m/s] 의 단위를 가지니까,
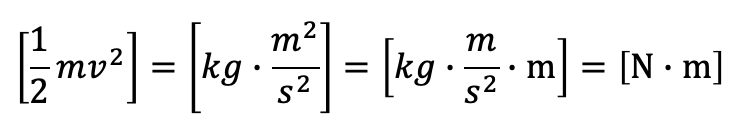
이렇게, 운동에너지로 정의한 양도 에너지와 같은 단위를 가짐을 알 수 있다.
이제 새로 도입한 운동에너지로 위의 식을 좀 간단히 쓰면,

외부의 힘이 계에 한 일은 계의 운동에너지의 변화량과 같다. 바꿔 말하면, 계의 최종 운동에너지는 계의 초기 운동에너지와 힘이 한 일의 합으로 표현된다.
이 관계가 바로 일-운동에너지 정리 (Work-Kinetic energy theorem) 이고, 교재에는 다음으로 설명되어있다.
When work is done on a system and the only change in the system is in its speed, the net work done on the system equals the change in kinetic energy of the system.
계에 일이 작용했을때, 그 결과로 계의 속력만 변했다면, 계에 작용한 일과 계의 운동에너지 변화량은 같다.
이를 바탕으로, 일의 크기가 양수이면, 계의 속력은 커지고, 음수이면 계의 속력이 감소 할 것이라는 생각을 할 수 있다.
[033-06] 계의 포텐셜 에너지 - Potential
책을 들어올리는 일에 대한 이야기로 시작해보자.

하나의 물체에 힘이 하는 일을 다뤘던 앞의 내용과 달리 지금 우리의 관심은 중력으로 상호작용하는 책과 지구로 구성된 계에 관한 것으로 바뀌었고, 책의 위치를 바꾸기 위해 (들어올리기위해) 우리가 계에 한 일을 에너지의 전달 관점에서 보면, 지구-책 계의 에너지의 증가로 반영되어야 할 것이다.
운동에너지 이야기와 가장 큰 차이는 책의 위치만 바뀌었지, 속력의 변화가 발생하지 않는다는 사실이다. 책은 처음위치에서나 최종위치에서나 정지상태이고, 변화한 계의 에너지가 운동에너지의 형태가 아니어서 일-운동에너지 정리는 적용이 불가능하다. 변화한 계의 에너지는 운동에너지의 개념과는 다른 일종의 '에너지 저장소 (energy storage)' 같은 형태로 나타나야 한다.
이제 아주 자연스러운 상상을 해보자. 들어올렸던 책을 놓으면, 책은 아래로 떨어지면서 처음의 위치로 돌아가게 될텐데, 이 때 책은 (지구-책 계는) 운동에너지를 갖게되고, 이 운동에너지의 근원은 책을 들어올리느라 계에 해준 일 이다. 책이 가장 높은 위치에 정지해 있는 동안, 계는 운동에너지를 가질 수 있는 포텐셜 (가능성, 잠재력) 을 가진다. 이를 바탕으로 책이 떨어지기 이전과 같이 에너지가 저장되는 메커니즘을 포텐셜 에너지 (Potential Energy) 라고 한다. 포텐셜 에너지는 둘 이상의 구성요소가 힘으로 상호작용하는 계에 적용 가능한 개념이다.
오해하지 말아햐 할 것은, 계가 포텐셜 에너지를 갖는다는 것이 다른 형태의 에너지 또는 에너지 자체를 가질 수 있는 잠재력을 의미하는게 아니라는 것이다. 포텐셜 에너지도 에너지이다.
포텐셜 에너지의 크기는 책의 위치 변화에서 알 수 있듯, 계의 구성요소들의 상대적 배치 (configuration) 에 의해 결정된다. 구성요소의 위치 변화, 회전에 의한 배치 변화는 포텐션 에너지의 변화를 의미한다.
이제 지구-책 계의 포텐셜 에너지를 표현하는 기호를 알아보자. 책의 질량이 m 이고, 책의 위치가 변하는 과정이 가속도의 발생 없이 아주 느리게 진행된다면, 책을 들어올리기 위해 필요한 힘은 책에 작용하는 중력의 크기와 같을 것으로 생각 할 수 있다. 힘의 크기와 변위를 알았으니까 일의 정의에 적용해보자.

위 식에서 갓을 쓰고 있는 j 는 위쪽 방향을 갖고 크기가 1 인 단위벡터이다. 계에 mg 의 크기를 갖는 힘이 위쪽 방향으로 작용해서, 높이의 차이 만큼 위쪽 방향으로 변위를 발생시켰다 라고 이해하면 된다.
위의 포텐셜 에너지는 중력에 대해 한 일 이므로 콕 집어 중력 포텐셜 에너지 (gravitational potential energy : Ug) 라 하고, 그 크기는 mgy 이다. 포텐셜 에너지를 나타내는 기호는 U 를 가장 많이 사용한다. 포텐셜 역시 에너지 이므로 다른 에너지와 마찬가지로 줄을 단위로 가지는데, 이게 맞는지 궁금하면 운동에너지에서 한것과 같은 과정으로 단위를 환산해보면 된다.
운동에너지의 변화량이 일의 크기와 같았던 것 처럼, 계의 포텐셜 에너지의 변화량도 일의 크기와 같다.
[033-07] 보존력과 비보존력
이제 계가 가질 수 있는 에너지의 세 번째 타입을 알아 보려고 하는데, 교재에서는 책을 밀어서 움직이는 상황을 고려해서 설명을 시작하지만, 이번 내용이 충분히 많고, 좀 편하게 내용을 시작하기위해 약간 다른 상황을 고려하고자 한다.
원시인들이 뾰족한 나무를 손바닥으로 열심히 회전시켜 불을 얻는 장면을 본 적이 있을텐데, 여기서 계에 해준 일은 계의 운동상태를 바꾸거나, 구성을 변화시키는데 쓰이지 않고, 계의 온도를 변화시키는데 쓰였다. 이와같이 계의 온도에 관련된 에너지를 내부에너지 (E int) 라 부른다. (내부 에너지에 대한 이야기는 나중에 자세히 다루게 된다.)
계 사이의 비보존력 : nonconservative force 을 에너지 변환 메커니즘으로 간주 할 수 있고, 비보존력은 계의 운동에너지를 내부에너지로 변환시킨다.
같은높이만큼 들어 올려진 책이 바닥으로 자유낙하 하는 경우와 빗면을 따라 미끄러져 내려오는 경우를 생각해보자. 두 상황의 들어올려진 책이 갖는 포텐셜 에너지는 같지만, 운동을 시작하면 얘기가 달라진다. 미끄러지는 책은 마찰에 의해 포텐셜 에너지의 일부가 내부 에너지로 전환되기 때문이다. 즉, 중력에 의해 자유낙하 하는 경우에는 경로의 영향을 받지 않지만, 미끄러지는 책은 마찰을 고려해야 하기 때문에 경로에 따른 차이가 발생한다. 이 때, 중력은 보존력, 마찰력은 비보존력으로 구분하며, 각각은 다음의 특징을 갖는다.
보존력 (Conservative forces)
1. The work done by a conservative force on a particle moving between any two points is independent of the path taken by the particle.
2. The work done by a conservative force on a particle moving through any closed path is zero. (A closed path is one for which the beginning point and the endpoint are identical.)
1. 두 지점 사이를 이동하는 입자에 보존력이 한 일은 입자가 움직인 경로에 무관하다.
2. 닫힌경로를 따라 움직이는 입자에 보존력이 한 일은 0 이다. (닫힌경로는 시작점과 끝점이 같은 경로이다.)
중력은 보존력이고, 위의 특성을 확인하기 좋은 예 이다. 지구 표면 근처에서 위치가 달라지는 물체에 중력이 한 일을 식으로 표현하면,

보다시피, 중력이 한 일은 물체의 처음과 나중위치에만 의존하며, 두 위치 사이를 어떤 경로를 따라 움직였는지에 대한 사실은 포함되어 있지 않다. 또한, 얼마나 긴 시간 오르락 내리락 했든 마지막에 도착한 위치가 처음 위치와 같으면 중력이 한 일은 0 이다.
앞에서 포텐셜 에너지는 계의 구성 요소의 배치와 관련이 있다고 했는데, (예를들어, 지구-책 계에서 포텐셜 에너지의 증가는 책의 위치가 달라지는 효과를 준다.) 이는 보존력의 경우에만 적용 할 수 있는 이야기이다. 일반적으로 보존력이 한 일은 계의 구성요소의 배치에 영향을 주고, 그 크기는 계의 포텐셜 에너지의 변화에 음의 부호를 붙인것과 같다.

말도 어렵고 뭐 온통 이상한 표현들 뿐 인거 같은데, 지구-책 계를 생각해보자. 지금까지 이야기 한 대로 내부 에너지의 변화는 지구의 중력이 책에 한 일에 대한 이야기 였고, 이 말은 계를 구성하고 있는 구성요소 사이에 작용하는 힘과 그 힘이 한 일에 대한 이야기이다. 위 식의 일에 붙은 int (내부) 는 구성요소 사이에 발생하는 현상에 대한 설명이라는 의미를 갖는다.
비보존력 (Nonconservative forces)
우리는 계의 역학적 에너지(mechanical energy) 를 계가 갖는 운동에너지와 포텐셜 에너지의 합으로 정의해서 사용한다. 책이 자유낙하하는 지구-책 계를 생각해보면, 계의 역학적 에너지가 보존됨을 쉽게 알 수 있다. 감소하는 포텐셜 에너지가 온전히 운동에너지 변환되고, 그 합을 일정하다. 그런데, 비보존력은 이 역학적 에너지에 변화를 일으킨다.
골을 넣은 축구선수가 잔디밭을 무릎으로 미끄러지는 세리머니를 한다고 생각해보자. 깊이 생각하지 않아도 무릎과 종아리가 얼마나 뜨거워질지 알 수 있는데, 이는 달리던 축구 선수가 갖는 역학적 에너지 (운동에너지) 의 일부가 운동 마찰력에 의해 계의 내부에너지 (무릎과 종아리의 온도변화) 로 변환되었기 때문이고, 이러한 역할을 하는 운동 마찰력 (모든 마찰력) 은 비보존력으로 구분된다.
책상 위의 책을 밀어서 옮기거나, 물체에 힘을 작용해서 운동을 발생 시킬 때, 마찰을 고려하지 않는 이유가 여기에 있다. 비보존력인 마찰력을 포함하게 되면, 계의 역학적 에너지가 더 이상 보존되지 않는 것 처럼 보이고, 이런 상황을 물리적으로 설명하고, 수학적으로 표현하는 일은 생각보다 복잡하기 때문에 "상황을 좀 간단히 표현하고자" 마찰을 배제하고 현상을 다루는 것 이다.
[033-08] 정리
생각보다 내용이 너무 많이 길어졌는데, 보존력과 포텐셜 에너지의 관계와 에너지 다이어그램에 대한 내용은 일단 넣지 않았다.
포텐셜을 미분하면 보존력 (힘) 을 얻을 수 있다는게 둘의 관계에 대한 결과인데, 물리적으로 아주 중요한 사실이긴 하지만 미분과 적분의 의미를 잘 모르는 상태에서 식을 보는건 별 의미 없는 일이기도 하고, 수식은 좀 배제하고 싶어서 요청이 있거나, 꼭 필요한 상황이 되면 다시 다룰 생각이다.
에너지 다이어그램은 에너지가 표현되는 수식을 그래프로 그리면 끝이라 굳이 장황하게 설명하지 않기로 했다.
이번 내용의 골자는 힘과 운동을 계 (시스템) 와 에너지의 개념으로 접근하고 설명 할 수 있음이고, 이를 위해 힘과 힘이 한 일, 그리고 에너지 사이에 어떤 관계가 있는지 알아봤다.
[참고문헌]
주 교재 : Physics for Scientists and Engineers, 9th Edition, Serway/Jewett
'일반물리' 카테고리의 다른 글
| [035-09-01] 역학 : 선형 운동량과 충돌 : 선형 운동량 (Linear momentum) (0) | 2021.07.30 |
|---|---|
| [034] 역학 : 에너지 보존 - Conservation of Energy (2) | 2021.04.26 |
| [032] 역학 : 회전운동과 뉴턴법칙의 응용 - Mechanics : Circular motion and other applications of Newton's laws (0) | 2020.06.24 |
| [031.5] 등속원운동과 주기 운동 - Uniform circular motion & Periodic motion (0) | 2020.06.16 |
| [031] 역학 : 뉴턴의 운동 법칙 - Mechanics : The Law of Motion (0) | 2020.06.11 |